Đại Số Tuyến Tính

Posted Jan 10, 2025 Updated Jan 15, 2025

By Bui Quang Dat

27 min read

Đại Số Tuyến Tính

Đại số tuyến tính là một lĩnh vực quan trọng của toán học, tập trung vào nghiên cứu vector, ma trận và không gian vector. Trong machine learning, đại số tuyến tính đóng vai trò nền tảng, giúp mô hình hóa và giải quyết các bài toán phức tạp. Lưu ý rằng, nội dung blog là nội dung Đại số tuyến tính trong sách Machine Learning Cơ Bản của Vũ Hữu Tiệp nhưng đã được giảm tải kiến thức và thêm phần code để phủ hợp với kĩ sư AI.

1.1 Lưu ý về ký hiệu

Trong blog này, những số vô hướng được biểu diễn bởi các chữ cái in nghiêng và có thể viết hoa, ví dụ $x_1, N, y, k$. Các ma trận được biểu diễn bởi các chữ viết hoa in đậm, ví dụ $\mathbf{X, Y, W} $. Các vector được biểu diễn bởi các chữ cái thường in đậm, ví dụ $\mathbf{y}, \mathbf{x}_1 $. Nếu không giải thích gì thêm, các vector được mặc định hiểu là các vector cột.
Đối với vector, $\mathbf{x} = [x_1, x_2, \dots, x_n]$ được hiểu là một vector hàng, $\mathbf{x} = [x_1; x_2; \dots; x_n] $ được hiểu là vector cột. Chú ý sự khác nhau giữa dấu phẩy ($,$) và dấu chấm phẩy ($;$). Đây chính là ký hiệu được Matlab sử dụng. Nếu không giải thích gì thêm, một chữ cái viết thường in đậm được hiểu là một vector cột.
Tương tự, trong ma trận, $\mathbf{X} = [\mathbf{x}_1, \mathbf{x}_2, \dots,\mathbf{x}_n]$ được hiểu là các vector cột $\mathbf{x}_j$ được đặt cạnh nhau theo thứ tự từ trái qua phải để tạo ra ma trận $\mathbf{X}$. Trong khi $\mathbf{X} = [\mathbf{x}_1; \mathbf{x}_2; \dots; \mathbf{x}_m]$ được hiểu là các vector $\mathbf{x}_i$ được đặt chồng lên nhau theo thứ tự từ trên xuống dưới dể tạo ra ma trận $\mathbf{X}$. Các vector được ngầm hiểu là có kích thước phù hợp để có thể xếp cạnh hoặc xếp chồng lên nhau. Phần tử ở hàng thứ $i$, cột thứ $j$ được ký hiệu là x_ij.
Cho một ma trận $\mathbf{W}$, nếu không giải thích gì thêm, ta hiểu rằng $\mathbf{w}_i$ là vector cột thứ $i$ của ma trận đó. Chú ý sự tương ứng giữa ký tự viết hoa và viết thường.

1.2 Chuyển vị và Hermitian

Một phép toán quan trọng trong đại số tuyến tính là chuyển vị (transpose).
Cho một ma trận $\mathbf{A} \in \mathbb{R}^{m\times n}$, ta nói $\mathbf{B} \in \mathbb{R}^{n\times m}$ là chuyển vị (transpose) của $A$ nếu $b_{ij} = a_{ji},~\forall 1 \leq i \leq n, 1 \leq j\leq m$.
Một cách ngắn gọn, chuyển vị của một ma trận là một ma trận nhận được từ ma trận cũ thông qua phép phản xạ gương qua đường chéo chính của ma trận ban đầu. Toán tử chuyển vị thường được ký hiệu bởi chữ $T$. Ví dụ, chuyển vị của một vector $\mathbf{x}$ được ký hiệu là $\mathbf{x}^T$; chuyển vị của một ma trận $\mathbf{A}$ được ký hiệu là $\mathbf{A}^T$. Cụ thể:

\[\mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_m \end{bmatrix} \implies \mathbf{x}^T = [x_1 \, x_2 \, \dots \, x_m]; \quad \mathbf{A} = \begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{bmatrix} \implies \mathbf{A}^T = \begin{bmatrix} a_{11} & a_{21} & \dots & a_{m1} \\ a_{12} & a_{22} & \dots & a_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \dots & a_{mn} \end{bmatrix}.\]

Nếu $\mathbf{A} \in \mathbb{R}^{m\times n}$ thì $\mathbf{A}^T \in \mathbb{R}^{n\times m}$. Nếu $\mathbf{A}^T = \mathbf{A}$, ta nói $\mathbf{A}$ là một ma trận đối xứng (symmetric matrix ).
Để tìm ma trận chuyển vị của một ma trận cho trước trong python, chúng ta có thể dùng thuộc tính .T trước ma trận cần chuyển:

  
import numpy as np

# Tạo một ma trận
A = np.array([[1, 2, 3], 
              [4, 5, 6]])

# Tính ma trận chuyển vị
A_T = A.T

print("Ma trận gốc:")
print(A)

print("\nMa trận chuyển vị:")
print(A_T)

Hoặc có thể dùng hàm numpy.transpose():

  
import numpy as np

# Tạo một ma trận
A = np.array([[1, 2, 3], 
              [4, 5, 6]])

# Tính ma trận chuyển vị
A_T = np.transpose(A)

print("Ma trận gốc:")
print(A)

print("\nMa trận chuyển vị:")
print(A_T)

Trong trường hợp vector hay ma trận có các phần tử là số phức, việc lấy chuyển vị thường đi kèm với việc lấy liên hợp phức. Tức là ngoài việc đổi vị trí của các phần tử, ta còn lấy liên hợp phức của các phần tử đó. Tên gọi của phép toán chuyển vị và lấy liên hợp này còn được gọi là chuyển vị liên hợp (conjugate transpose), và thường được ký hiệu bằng chữ $H$ thay cho chữ $T$. Chuyển vị liên hợp của một ma trận $\mathbf{A}$ được ký hiệu là $\mathbf{A}^H$, được đọc là $\mathbf{A}$ Hermitian.
Cho $\mathbf{A} \in \mathbb{C}^{m\times n}$, ta nói $\mathbf{B} \in \mathbb{C}^{n\times m}$ là chuyển vị liên hợp của $\mathbf{A}$ nếu $b_{ij} = \overline{a_{ji}},~\forall 1 \leq i \leq n, 1 \leq j \leq m$, trong đó $\overline{a}$ là liên hiệp phức của $a$.
Ví dụ:

\[\mathbf{A} = \begin{bmatrix} 1 + 2i & 3 - 4i \\ i & 2 \end{bmatrix} \implies \mathbf{A}^H = \begin{bmatrix} 1 - 2i & -i \\ 3 + 4i & 2 \end{bmatrix}; \quad \mathbf{x} = \begin{bmatrix} 2 + 3i \\ 2i \end{bmatrix} \implies \mathbf{x}^H = [2 - 3i \,\, -2i]\]

Nếu $\mathbf{A}, \mathbf{x}$ là các ma trận và vector thực thì $\mathbf{A}^H = \mathbf{A}^T, \mathbf{x}^H = \mathbf{x}^T$.
Nếu chuyển vị liên hợp của một ma trận vuông phức bằng với chính nó, $\mathbf{A}^H = \mathbf{A}$, ta nói ma trận đó là Hermitian.
Trong Python, để tính chuyển vị liên hợp, bạn cần sử dụng thuộc tính .T để chuyển vị và hàm numpy.conjugate() hoặc .conj() để lấy liên hợp phức:

  
import numpy as np

# Tạo một ma trận phức
A = np.array([[1+2j, 2-3j], 
              [3+4j, 4-5j]])

# Tính chuyển vị liên hợp
A_H = A.conj().T

print("Ma trận gốc:")
print(A)

print("\nChuyển vị liên hợp:")
print(A_H)

  
import numpy as np

# Tạo một ma trận phức
A = np.array([[1+2j, 2-3j], 
              [3+4j, 4-5j]])

# Tính chuyển vị liên hợp
A_H = np.transpose(np.conjugate(A))

print("Ma trận gốc:")
print(A)

print("\nChuyển vị liên hợp:")
print(A_H)

1.3 Phép nhân hai ma trận

Cho hai ma trận $\mathbf{A} \in \mathbb{R}^{m\times n}, \mathbf{B} \in \mathbb{R}^{n \times p}$, tích của hai ma trận được ký hiệu là $\mathbf{C} = \mathbf{A}\mathbf{B} \in \mathbb{R}^{m \times p}$ trong đó phần tử ở hàng thứ $i$, cột thứ $j$ của ma trận kết quả được tính bởi:

\[c_{ij} = \sum_{k=1}^na_{ik}b_{kj}, ~\forall 1\leq i \leq m, 1 \leq j \leq p\]

Để nhân được hai ma trận, số cột của ma trận thứ nhất phải bằng số hàng của ma trận thứ hai. Trong ví dụ trên, chúng đều bằng $n$.
Giả sử kích thước các ma trận là phù hợp để các phép nhân ma trận tồn tại, ta có một vài tính chất sau:
1. Phép nhân ma trận không có tính chất giao hoán. Thông thường (không phải luôn luôn), $\mathbf{A}\mathbf{B} \neq \mathbf{B}\mathbf{A}$. Thậm chí, trong nhiều trường hợp, các phép tính này không tồn tại vì kích thước các ma trận lệch nhau.
2. Phép nhân ma trận có tính chất kết hợp: $\mathbf{A}\mathbf{B}\mathbf{C} = (\mathbf{A}\mathbf{B})\mathbf{C} = \mathbf{A}(\mathbf{B}\mathbf{C})$.
3. Phép nhân ma trận có tính chất phân phối đối với phép cộng: $\mathbf{A}(\mathbf{B} + \mathbf{C}) = \mathbf{A}\mathbf{B} + \mathbf{A}\mathbf{C}$.
4. Chuyển vị của một tích bằng tích các chuyển vị theo thứ tự ngược lại. Điều tương tự xảy ra với Hermitian của một tích:

\[(\mathbf{A}\mathbf{B})^T = \mathbf{B}^T \mathbf{A}^T; \quad (\mathbf{A}\mathbf{B})^H = \mathbf{B}^H\mathbf{A}^H\]

Theo định nghĩa trên, bằng cách coi vector là một trường hợp đặc biệt của ma trận, tích vô hướng của hai vector (inner product) $\mathbf{x},\mathbf{y} \in \mathbb{R}^{n}$ được định nghĩa là:

\[\mathbf{x}^T\mathbf{y} = \mathbf{y}^T\mathbf{x} = \sum_{k=1}^nx_iy_i\]

Chú ý, $\mathbf{x}^H\mathbf{y} = (\mathbf{y}^H\mathbf{x})^H = \mathbf{y}^H\mathbf{x}$. Chúng bằng nhau khi và chỉ khi chúng là các số thực. Nếu tích vô hướng của hai vector khác không bằng không, hai vector đó vuông góc với nhau.
$\mathbf{x}^H\mathbf{x} \geq 0 ~\forall \mathbf{x} \in \mathbb{C}^{n}$ vì tích của một số phức với liên hiệp của nó luôn là một số không âm.
Phép nhân của một ma trận $\mathbf{A} \in \mathbb{R}^{m \times n}$ với một vector $\mathbf{x} \in \mathbb{R}^{n}$ là một vector $\mathbf{b} \in \mathbb{R}^{m}$:

\[\mathbf{A}\mathbf{x} = \mathbf{b}, ~\text{với} ~b_i = \mathbf{A}_{i,:}\mathbf{x}\]

Với $\mathbf{A}_{i,:}$ là vector hàng thứ $i$ của $\mathbf{A}$.
Trong Python, bạn có thể thực hiện phép nhân hai ma trận bằng cách sử dụng thư viện NumPy. NumPy cung cấp vài cách sau để nhân ma trận: @, numpy.dot(), numpy.matmul():

  
import numpy as np

# Tạo hai ma trận
A = np.array([[1, 2], 
              [3, 4]])

B = np.array([[5, 6], 
              [7, 8]])

# Phép nhân ma trận
C = A @ B

print("Kết quả phép nhân ma trận:")
print(C)
C = np.dot(A, B)

print("Kết quả phép nhân ma trận:")
print(C)

C = np.matmul(A, B)

print("Kết quả phép nhân ma trận:")
print(C)

Ngoài ra, có một phép nhân khác được gọi là Hadamard (hay element-wise) hay được sử dụng trong Machine Learning. Tích Hadamard của hai ma trận cùng kích thước $\mathbf{A}, \mathbf{B} \in \mathbb{R}^{m\times n}$, ký hiệu là $\mathbf{C} = \mathbf{A} \odot \mathbf{B} \in \mathbb{R}^{m \times n}$, trong đó:

\[c_{ij} = a_{ij}b_{ij}\]

Trong python, để tính tích Hadamard, bạn có thể sử dụng toán tử * hoặc hàm numpy.multiply():

  
import numpy as np

# Tạo hai ma trận
A = np.array([[1, 2], 
              [3, 4]])

B = np.array([[5, 6], 
              [7, 8]])

# Tích Hadamard
C = A * B

print("Tích Hadamard:")
print(C)

C = np.multiply(A, B)

print("Tích Hadamard:")
print(C)

1.4 Ma trận đơn vị và ma trận nghịch đảo

1.4.1 Ma trận đơn vị

Đường chéo chính của một ma trận là tập hợp các điểm có chỉ số hàng và cột bằng nhau. Cách định nghĩa này cũng có thể được áp dụng cho một ma trận không vuông. Cụ thể, nếu $\mathbf{A} \in \mathbb{R}^{m \times n}$ thì đường chéo chính của $\mathbf{A}$ bao gồm $(a_{11}, a_{22}, \dots, a_{pp})$, trong đó $p = \min(m, n)$.
Một ma trận đơn vị bậc $n$ là một ma trận đặc biệt trong $\mathbb{R}^{n\times n}$ với các phần tử trên đường chéo chính bằng 1, các phần tử còn lại bằng 0. Ma trận đơn vị thường được ký hiệu là $\mathbf{I}$ (identity matrix). Khi làm việc với nhiều ma trận đơn vị với bậc khác nhau, ta thường ký kiệu $\mathbf{I}_n$ cho ma trận đơn vị bậc $n$. Dưới đây là các ma trận đơn vị bậc 3 và bậc 4:

\[\mathbf{I}_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \quad \mathbf{I}_4 = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}.\]

Ma trận đơn vị có một tính chất đặc biệt trong phép nhân. Nếu $\mathbf{A} \in \mathbb{R}^{m\times n}, \mathbf{B} \in \mathbb{R}^{n\times m}$ và $\mathbf{I}$ là ma trận đơn vị bậc $n$, ta có: $\mathbf{A}\mathbf{I}= \mathbf{A}, \mathbf{I}\mathbf{B} = \mathbf{B}$.
Với mọi vector $\mathbf{x} \in \mathbb{R}^n$, ta có $\mathbf{I}_n \mathbf{x} = \mathbf{x}$.
Trong Python, bạn có thể tạo ma trận đơn vị (identity matrix) bằng cách sử dụng các hàm sau: numpy.eye(), numpy.identity():

  
import numpy as np

# Tạo ma trận đơn vị 3x3
I = np.eye(3)

print("Ma trận đơn vị 3x3:")
print(I)

I = np.identity(4)

print("Ma trận đơn vị 4x4:")
print(I)

Ngoài ra, numpy.eye(N, M=None) cho phép tạo ma trận có dạng giống ma trận đơn vị nhưng có thể chỉ định số hàng và số cột khác nhau (không nhất thiết là vuông).

  
I = np.eye(3, 4)
print(I)

1.4.2. Ma trận nghịch đảo

Cho một ma trận vuông $\mathbf{A} \in \mathbb{R}^{n\times n }$, nếu tồn tại một ma trận vuông $\mathbf{B} \in \mathbb{R}^{n\times n}$ sao cho $\mathbf{A}\mathbf{B} = \mathbf{I} _n$, ta nói $\mathbf{A}$ là khả nghịch, và $\mathbf{B}$ được gọi là ma trận nghịch đảo của $\mathbf{A}$. Nếu không tồn tại ma trận $\mathbf{B}$ thoả mãn điều kiện trên, ta nói rằng ma trận $\mathbf{A}$ là không khả nghịch.
Nếu $\mathbf{A}$ khả nghịch, ma trận nghịch đảo của nó được ký hiệu là $\mathbf{A}^{-1}$. Ta cũng có:

\[\mathbf{A}^{-1}\mathbf{A} = \mathbf{A}\mathbf{A}^{-1} = \mathbf{I}\]

Ma trận nghịch đảo thường được sử dụng để giải hệ phương trình tuyến tính. Giả sử $\mathbf{A} \in \mathbb{R}^{n\times n}$ là một ma trận khả nghịch và $\mathbf{b}$ là một vector bất kỳ trong $\mathbb{R}^n$. Khi đó, phương trình:

\[\mathbf{A}\mathbf{x} = \mathbf{b}\]

Có nghiệm duy nhất $\mathbf{x} = \mathbf{A}^{-1}\mathbf{b}$. Thật vậy, nhân bên trái cả hai vế của phương trình với $\mathbf{A}^{-1}$, ta có $\mathbf{A}\mathbf{x} = \mathbf{b} \Leftrightarrow \mathbf{A}^{-1}\mathbf{A}\mathbf{x} = \mathbf{A}^{-1}\mathbf{b} \Leftrightarrow \mathbf{x} = \mathbf{A}^{-1}\mathbf{b}$.
Nếu $\mathbf{A}$ không khả nghịch, thậm chí không vuông, phương trình tuyến tính $\mathbf{A}\mathbf{x} = \mathbf{b}$ có thể không có nghiệm hoặc có vô số nghiệm.
Giả sử các ma trận vuông $\mathbf{A}, \mathbf{B}$ là khả nghịch, khi đó tích của chúng cũng khả nghịch, và $(\mathbf{A}\mathbf{B})^{-1} = \mathbf{B}^{-1}\mathbf{A}^{-1}$. Quy tắc này cũng giống với cách tính ma trận chuyển vị của tích các ma trận.
Công thức tổng quát tính ma trận nghịch đảo là:

\[\mathbf{A}^{-1} = \frac{1}{\det(\mathbf{A})} \cdot \text{adj}(\mathbf{A})\]

Trong đó: $\det(\mathbf{A})$ được gọi là định thức của ma trận $\mathbf{A}$, $\text{adj}(\mathbf{A})$ là ma trận phụ hợp của ma trận $\mathbf{A}$. Phần tính định thức sẽ được trình bày ở phần sau, còn phần tính ma trận phụ hợp thì bạn có thể lên mạng xem phần này.
Để tính ma trận nghịch đảo trong python, chúng ta có thể sử dụng hàm numpy.linalg.inv():

  
import numpy as np

# Tạo ma trận vuông
A = np.array([[4, 7],
              [2, 6]])
# Tính ma trận nghịch đảo
A_inv = np.linalg.inv(A)
print("Ma trận gốc:")
print(A)
print("\nMa trận nghịch đảo:")
print(A_inv)

Nếu ma trận $\mathbf{A}$ không khả nghịch (định thức = 0), NumPy sẽ ném lỗi LinAlgError. Bạn có thể xử lý lỗi này như sau:

  
import numpy as np

# Tạo ma trận không khả nghịch
B = np.array([[1, 2],
              [2, 4]])  # Định thức = 0

try:
    B_inv = np.linalg.inv(B)
    print("Ma trận nghịch đảo của B:")
    print(B_inv)
except np.linalg.LinAlgError:
    print("Ma trận không khả nghịch.")

Ngoài ra nếu ma trận $\mathbf{A}$ không khả nghịch thì người ta có them một khái niệm nữa đó chính là ma trận giả nghịch đảo $\mathbf{A}^{\dagger}$ (đọc là A dagger trong tiếng Anh). Vì cách tính ma trận giả nghịch đảo khá là phức tạp nên tôi sẽ không đề cập đến, bạn có thể xem tại đây. Trong Python, bạn có thể tính ma trận giả nghịch đảo bằng cách sử dụng hàm numpy.linalg.pinv() trong thư viện.

  
import numpy as np

# Tạo một ma trận
A = np.array([[1, 2],
              [3, 4],
              [5, 6]])

# Tính ma trận giả nghịch đảo
A_pinv = np.linalg.pinv(A)

print("Ma trận gốc:")
print(A)

print("\nMa trận giả nghịch đảo:")
print(A_pinv)

1.5 Một vài ma trận đặc biệt khác

1.5.1 Ma trận đường chéo

Ma trận đường chéo (diagonal matrix ) là ma trận chỉ có các thành phần trên đường chéo chính là khác không. Định nghĩa này cũng có thể được áp dụng lên các ma trận không vuông.Ma trận không (tất cả các phần tử bằng 0) và đơn vị là các ma trận đường chéo. Một vài ví dụ về các ma trận đường chéo:

\[[1], \begin{bmatrix} 2 & 0 \\ 0 & 0 \end{bmatrix}, \begin{bmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 0 \end{bmatrix}, \begin{bmatrix} -1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 0 \end{bmatrix}.\]

Với các ma trận đường chéo vuông, thay vì viết cả ma trận, ta có thể chỉ liệt kê các thành phần trên đường chéo chính. Ví dụ, một ma trận đường chéo vuông $\mathbf{A} \in \mathbb{R}^{m\times m}$ có thể được ký hiệu là $\text{diag}(a_{11}, a_{22}, \dots, a_{mm})$ với $a_{ii}$ là phần tử hàng thứ $i$, cột thứ $i$ của ma trận $\mathbf{A}$.
Tích, tổng của hai ma trận đường chéo vuông cùng bậc là một ma trận đường chéo. Một ma trận đường chéo vuông là khả nghịch khi và chỉ khi mọi phần tử trên đường chéo chính của nó khác không. Nghịch đảo của một ma trận đường chéo khả nghịch cũng là một ma trận đường chéo. Cụ thể hơn, $(\text{diag}(a_1, a_2, \dots, a_n))^{-1} = \text{diag}(a_1^{-1}, a_2^{-1}, \dots, a_n^{-1})$.
Trong Python, bạn có thể tạo một ma trận đường chéo bằng cách sử dụng hàm np.diag như sau:

  
import numpy as np
# Danh sách giá trị trên đường chéo
diagonal_values = [1, 2, 3, 4]
# Tạo ma trận đường chéo
diagonal_matrix = np.diag(diagonal_values)
print("Ma trận đường chéo:")
print(diagonal_matrix)

1.5.2 Ma trận tam giác

Một ma trận vuông được gọi là ma trận tam giác trên nếu tất cả các thành phần nằm phía dưới đường chéo chính bằng 0. Tương tự, một ma trận vuông được gọi là ma trận tam giác dưới nếu tất cả các thành phần nằm phía trên đường chéo chính bằng 0.
Các hệ phương trình tuyến tính với ma trận hệ số ở dạng tam giác (trên hoặc dưới) có thể được giải mà không cần tính ma trận nghịch đảo. Xét hệ:

\[\begin{equation} \left\{ \begin{matrix} a_{11}x_1 + &a_{12}x_2 + &\dots + &a_{1,n-1}x_{n-1} + & a_{1n}x_n= & b_1 \\ &a_{22}x_2 + &\dots + &a_{2, n-1}x_{n-2} + &a_{2n}x_n = & b_2 \\ &\dots & \dots & \dots & \dots \\ & & &a_{n-1,n-1}x_{n-1} + &a_{n-1, n}x_n = & b_{n-1} \\ & & & &a_{nn}x_n = & b_{n} \\ \end{matrix} \right. \end{equation}\]

Hệ này có thể được viết gọn dưới dạng $\mathbf{A}\mathbf{x} = \mathbf{b}$ với $\mathbf{A}$ là một ma trận tam giác trên. Nhận thấy rằng phương trình này có thể giải mà không cần tính ma trận nghịch đảo $\mathbf{A}^{-1}$. Thật vậy, ta có thể giải $x_n$ dựa vào phương trình cuối cùng. Tiếp theo, $x_{n-1}$ có thể được tìm bằng cách thay $x_n$ vào phương trình thứ hai từ cuối. Tiếp tục quá trình này, ta sẽ có nghiệm cuối cùng $\mathbf{x}$. Quá trình giải từ cuối lên đầu và thay toàn bộ các thành phần đã tìm được vào phương trình hiện tại được gọi là phép thế ngược. Nếu ma trận hệ số là một ma trận tam giác dưới, hệ phương trình có thể được giải bằng một quá trình ngược lại lần - lượt tính $x_1$ rồi $x_2, \dots, x_n$. Quá trình này được gọi là phép thế xuôi.

1.6 Định thức

1.6.1 Định nghĩa

Định thức của một ma trận vuông $\mathbf{A}$ được ký hiệu là $\det(\mathbf{A})$ hoặc $\det\mathbf{A}$. Có nhiều cách định nghĩa khác nhau của định thức. Chúng ta sẽ sử dụng cách định nghĩa dựa trên quy nạp theo bậc $n$ của ma trận.
Với $n = 1$, $\det(\mathbf{A})$ chính bằng phần tử duy nhất của ma trận đó.
Với một ma trận vuông bậc $n>1$:

\[\begin{equation} \mathbf{A} = \left[ \begin{matrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \dots & \dots & \ddots & \dots \\ a_{n1} & a_{n2} & \dots & a_{nn} \end{matrix} \right] \Rightarrow \det(\mathbf{A}) = \sum_{j=1}^n (-1)^{i+j} a_{ij}\det(\mathbf{A}_{ij}) \end{equation}\]

Trong đó $1 \leq i \leq n$ bất kỳ và $\mathbf{A}_{ij}$ là phần bù đại số của $\mathbf{A}$ ứng với phần tử ở hàng $i$, cột $j$. Phần bù đại số này là một ma trận con của $\mathbf{A}$, nhận được từ $\mathbf{A}$ bằng cách xoá hàng thứ $i$ và cột thứ $j$ của nó. Đây chính là cách tính định thức dựa trên cách khai triển hàng thứ $i$ của ma trận.

1.6.2 Tính chất

$\det(\mathbf{A}) = \det(\mathbf{A}^T)$: Một ma trận vuông bất kỳ và chuyển vị của nó có định thức như nhau.
Định thức của một ma trận đường chéo vuông bằng tích các phần tử trên đường chéo chính. Nói cách khác, nếu $\mathbf{A} = \text{diag}(a_1, a_2, \dots, a_n)$ thì $\det(\mathbf{A}) = a_1a_2\dots a_n$.
Định thức của một ma trận đơn vị bằng 1.
Định thức của một ma trận đơn vị bằng 1.

\[\det(\mathbf{A}\mathbf{B}) = \det(\mathbf{A}) \det(\mathbf{B})\]

Nếu một ma trận có một hàng hoặc một cột là một vector $\mathbf{0}$, thì định thức của nó bằng 0.
Một ma trận là khả nghịch khi và chỉ khi định thức của nó khác 0.
Nếu một ma trận khả nghịch, định thức của ma trận nghịch đảo của nó bằng nghịch đảo định thức của nó.

\[\begin{equation} \det(\mathbf{A}^{-1}) = \frac{1}{\det(\mathbf{A})} ~\text{vì}~ \det(\mathbf{A}) \det(\mathbf{A}^ {-1}) = \det(\mathbf{A} \mathbf{A}^{-1}) = \det(\mathbf{I}) = 1. \end{equation}\]

Để tính định thức của một ma trận trong Python, bạn có thể sử dụng thư viện NumPy, cụ thể là hàm numpy.linalg.det:

  
import numpy as np

# Ma trận vuông
matrix = np.array([[1, 2, 3],
                   [4, 5, 6],
                   [7, 8, 9]])

# Tính định thức
determinant = np.linalg.det(matrix)

print("Định thức của ma trận là:", determinant)

1.7 Chuẩn của vector và ma trận

Trong không gian một chiều, khoảng cách giữa hai điểm là trị tuyệt đối của hiệu giữa hai giá trị đó. Trong không gian hai chiều, tức mặt phẳng, chúng ta thường dùng khoảng cách Euclid để đo khoảng cách giữa hai điểm. Khoảng cách Euclid chính là độ dài đoạn thẳng nối hai điểm trong mặt phẳng. Đôi khi, để đi từ một điểm này tới một điểm kia, chúng ta không thể đi bằng đường thẳng vì còn phụ thuộc vào hình dạng đường đi nối giữa hai điểm.
Việc đo khoảng cách giữa hai điểm dữ liệu nhiều chiều rất cần thiết trong machine learning. Đây chính là lý do khái niệm chuẩn (norm) ra đời. Để xác định khoảng cách giữa hai vector $\mathbf{y}$ và $\mathbf{z}$, người ta thường áp dụng một hàm số lên vector hiệu $\mathbf{x = y - z}$. Hàm số này cần có một vài tính chất đặc biệt.

Điều kiện thứ nhất là dễ hiểu vì khoảng cách không thể là một số âm. Hơn nữa, khoảng cách giữa hai điểm $\mathbf{y}$ và $\mathbf{z}$ bằng 0 khi và chỉ khi hai điểm đó trùng nhau, tức $\mathbf{x = y - z = 0}$.
Điều kiện thứ hai cũng có thể được lý giải như sau. Nếu ba điểm $\mathbf{y, v}$ và $\mathbf{z}$ thẳng hàng, hơn nữa $\mathbf{v - y} = \alpha (\mathbf{v - z})$ thì khoảng cách giữa $\mathbf{v}$ và $\mathbf{y}$ gấp $\alpha$ lần khoảng cách giữa $\mathbf{v}$ và $\mathbf{z}$.
Điều kiện thứ ba chính là bất đẳng thức tam giác nếu ta coi $\mathbf{x}_1 = \mathbf{y - w}, \mathbf{x}_2 = \mathbf{w - z} $ với $\mathbf{w}$ là một điểm bất kỳ trong cùng không gian.

1.7.1 Một số chuẩn vector thường dùng

Độ dài Euclid của một vector $\mathbf{x} \in \mathbb{R}^n$ chính là một norm, norm này được gọi là $\ell_2$ norm hoặc chuẩn Euclidean norm:

\[\begin{equation} \label{eqn:norm2} \|\mathbf{x}\|_2 = \sqrt{x_1^2 + x_2^2 + \dots + x_n^2} \end{equation}\]

Bình phương của chuẩn $\ell_2$ chính là tích vô hướng của một vector với chính nó, $|\mathbf{x}|_2^2 = \mathbf{x}^T\mathbf{x}$. Với $p$ là một số không nhỏ hơn 1 bất kỳ, hàm số:

\[\begin{equation} \label{eqn:normp} \|\mathbf{x}\|_p = (|x_1|^p + |x_2|^p + \dots |x_n|^p)^{\frac{1}{p}} \end{equation}\]

Được chứng minh thỏa mãn ba điều kiện của chuẩn, và được gọi là $\ell_p$ norm.
Có một vài giá trị của $p$ thường được dùng:
1. Khi $p = 2$, ta có $\ell_2$ norm như ở trên.
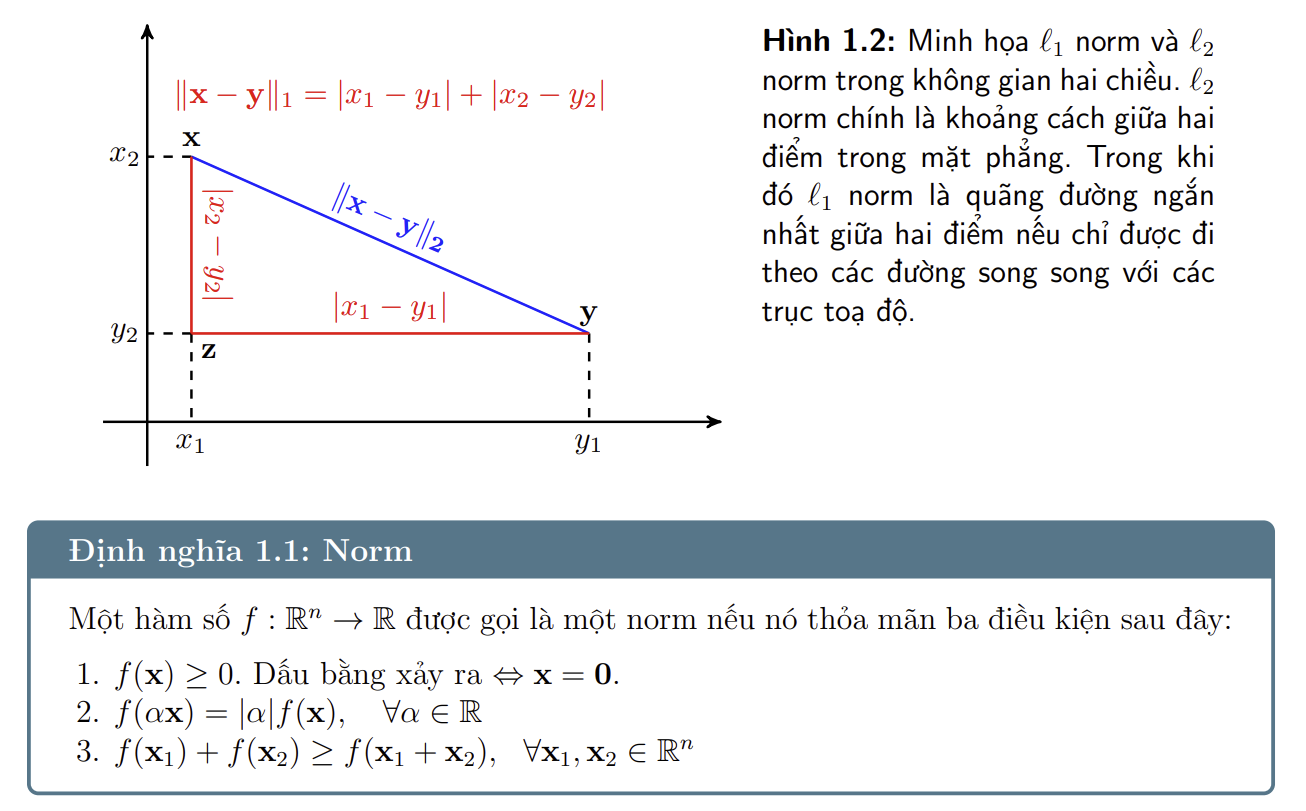
2. Khi $p = 1$, ta có $\ell_1$ norm:

\[\|\mathbf{x}\|_1 = |x_1| + |x_2| + \cdots + |x_n|\]

Là tổng các trị tuyệt đối của từng phần tử của $\mathbf{x}$. Hình 1.2 là một ví dụ sánh chuẩn $\ell_1$ và chuẩn $\ell_2$ trong không gian hai chiều. Norm 2 (màu xanh) chính là đường thằng chim bay nối giữa hai vector $\mathbf{x}$ và $\mathbf{y}$. Khoảng cách $\ell_1$ norm giữa hai điểm này (màu đỏ) có thể diễn giải như là đường đi từ $\mathbf{x}$ tới $\mathbf{y}$ trong một thành phố mà đường phố tạo thành hình bàn cờ. Chúng ta chỉ có cách đi dọc theo cạnh của bàn cờ mà không được đi thẳng như đường chim bay.

Khi $p \to \infty$, giả sử $i = \arg\max_{j = 1, 2, \ldots, n} |x_j|$ Khi đó:

\[\begin{equation} \|\mathbf{x}\|_p = |x_i|\left(1 + \left|\frac{x_1}{x_i}\right|^p + \dots + \left|\frac{x_{i-1}}{x_i}\right|^p + \left|\frac{x_{i+1}}{x_i}\right|^p + \dots +\left|\frac{x_{n}}{x_i}\right|^p\right)^{\frac{1} {p}} \end{equation}\]

Ta thấy rằng:

\[\begin{equation} \lim_{p \rightarrow \infty}\left(1 + \left|\frac{x_1}{x_i}\right|^p + \dots + \left|\frac{x_{i-1}}{x_i}\right|^p + \left|\frac{x_{i+1}}{x_i}\right|^p + \dots +\left|\frac{x_{n}}{x_i}\right|^p\right)^{\frac{1}{p}} = 1 \end{equation}\]

Vì đại lượng trong dấu ngoặc đơn không vượt quá $n$. Ta có:

\[\begin{equation} \|\mathbf{x}\|_{\infty} \triangleq \lim_{p \rightarrow \infty} \|\mathbf{x}\|_{p} = |x_i| = \max_{j=1, 2, \dots, n} | x_j| \end{equation}\]

Bạn có thể dùng hàm numpy.linalg.norm để tính chuẩn $\ell_p$ như sau:

  
import numpy as np

p = 2 # chuẩn p, đặt là np.inf nếu muốn tính chuẩn vô cùng
# Vector
v = np.array([3, 4])

# Tính chuẩn Lp
l2_norm = np.linalg.norm(v,p)

print(f"Chuẩn L{p} của vector v:", l2_norm)

1.7.2 Chuẩn Frobenius của ma trận

Với một ma trận $\mathbf{A} \in \mathbb{R}^{m\times n}$, chuẩn thường được dùng nhất là chuẩn Frobenius, ký hiệu là $|\mathbf{A}|_F$, là căn bậc hai của tổng bình phương tất cả các phần tử của nó:

\[\begin{equation*} \|\mathbf{A}\|_F = \sqrt{\sum_{i = 1}^m \sum_{j = 1}^n a_{ij}^2} \end{equation*}\]

Chú ý rằng chuẩn $\ell_2$, $||\mathbf{A}||_2$, là một chuẩn khác của ma trận, không phổ biến bằng chuẩn Frobenius.
Bạn có thể sử dụng hàm numpy.linalg.norm để tính chuẩn Frobenius như sau:

  
import numpy as np

# Khởi tạo ma trận
A = np.array([[1, 2], [3, 4]])

# Tính chuẩn Frobenius
frobenius_norm = np.linalg.norm(A, 'fro')

print("Chuẩn Frobenius của ma trận A:", frobenius_norm)

1.7.3 Vết của ma trận

Vết (trace) của một ma trận vuông là tổng tất cả cả phần tử trên đường chéo chính của nó.
Vết của một ma trận được $\mathbf{A}$ được ký hiệu là $\text{trace}(\mathbf{A})$. Hàm số trace xác định trên tập các ma trận vuông được sử dụng rất nhiều trong tối ưu vì những tính chất đẹp của nó.
Các tính chất quan trọng của hàm vết, với giả sử rằng các ma trận trong hàm trace là vuông và các phép nhân ma trận thực hiện được:
1. Một ma trận vuông bất kỳ và chuyển vị của nó có vết bằng nhau: $\text{trace}(\mathbf{A}) = \text{trace}(\mathbf{A}^T)$. Việc này được suy ra từ việc phép chuyển vị không làm thay đổi các phần tử trên đường chéo chính của một ma trận.
2. Vết của một tổng bằng tổng các vết:

\[\displaystyle\text{trace}(\sum_{i=1}^k \mathbf{A}_i) = \sum_{i=1}^k \text{trace}(\mathbf{A}_i)\]

$\text{trace}(k\mathbf{A}) = k\text{trace}(\mathbf{A})$ với $k$ là một số vô hướng bất kỳ.
$\text{trace}(\mathbf{A}) = \sum_{i = 1}^D \lambda_i $ với $\mathbf{A}$ là một ma trận vuông và $\lambda_i, i = 1, 2, \dots, N$ là toàn bộ các trị riêng của nó, có thể lặp hoặc phức. Việc chứng minh tính chất này có thể được dựa trên ma trận đặc trưng của $\mathbf{A}$ và định lý Viète.
$\text{trace}(\mathbf{AB}) = \text{trace}(\mathbf{BA})$. Đẳng thức này được suy ra từ việc đa thức đặc trưng của $\mathbf{A}\mathbf{B}$ và $\mathbf{B}\mathbf{A}$ là như nhau. Bạn đọc cũng có thể chứng minh bằng cách tính trực tiếp các phần tử trên đường chéo chính của $\mathbf{A}\mathbf{B}$ và $\mathbf{B}\mathbf{A}$.
$\text{trace}(\mathbf{A}\mathbf{B}\mathbf{C}) = \text{trace}(\mathbf{B}\mathbf{C}\mathbf{A})$, nhưng $\text{trace}(\mathbf{A}\mathbf{B}\mathbf{C})$ không đồng nhất với $\text{trace}(\mathbf{A}\mathbf{C}\mathbf{B})$.
Nếu $\mathbf{X}$ là một ma trận khả nghịch cùng chiều với $\mathbf{A}$ thì:

\[\text{trace} (\mathbf{X}\mathbf{A}\mathbf{X}^{-1}) = \text{trace}(\mathbf{X}^{-1}\mathbf{X}\mathbf{A}) = \text{trace}(\mathbf{A})\]

$||\mathbf{A}||_F^2 = \text{trace}(\mathbf{A}^T\mathbf{A}) = \text{trace}(\mathbf{A}\mathbf{A}^T)$ với $\mathbf{A}$ là một ma trận bất kỳ. Từ đây ta cũng suy ra $\text{trace}(\mathbf{A}\mathbf{A}^T) \geq 0$ với mọi ma trận $\mathbf{A}$.

Bạn có thể dùng hàm numpy.trace để tính vết của ma trận như sau:

  
import numpy as np

# Khởi tạo ma trận
A = np.array([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9]])

# Tính vết của ma trận
trace_A = np.trace(A)

print("Vết của ma trận A:", trace_A)

1.8 Tổng Kết

Đại số tuyến tính là nền tảng quan trọng của AI, hỗ trợ biểu diễn và xử lý dữ liệu qua vector và ma trận. Từ học máy đến xử lý ảnh, ngôn ngữ tự nhiên, các phép toán như nhân ma trận, chuẩn hay phân rã ma trận giúp xây dựng và tối ưu hóa các mô hình AI hiện đại. Hiểu rõ đại số tuyến tính là chìa khóa để khám phá và ứng dụng hiệu quả trí tuệ nhân tạo trong thực tiễn.

Machine Learning

linear

This post is licensed under CC BY 4.0 by the author.