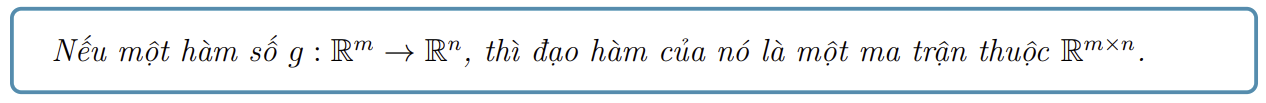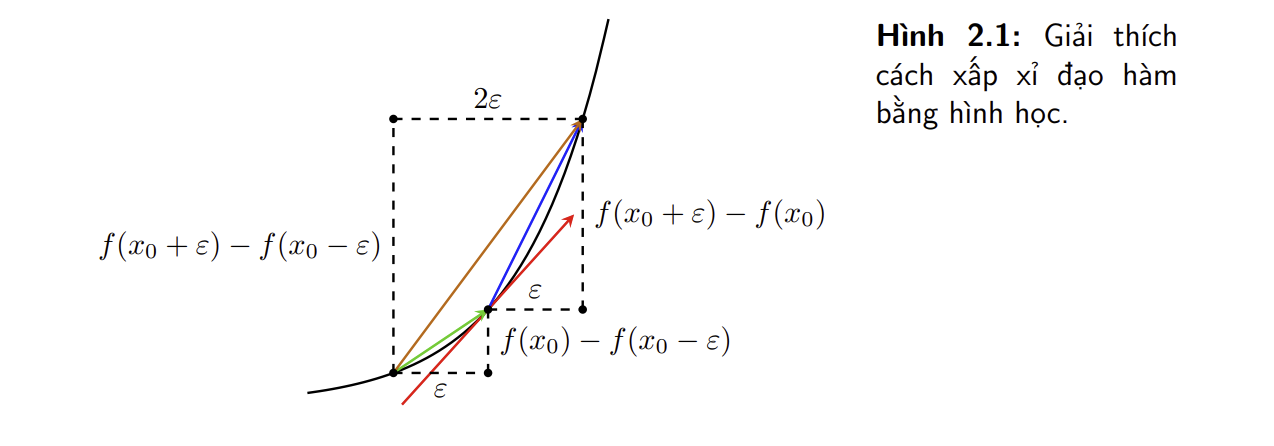Post

Giải Tích Ma Trận

Posted Updated
By Bui Quang Dat
14 min read
Giải Tích Ma Trận

Để hiểu được rõ các normal equation trong machine learning thì bạn bắt buộc phải biết được phần này. Blog này được giữ y nguyên của Chương 2: Giải tích ma trận trong sách Machine Learning Cơ Bản nhưng có thêm phần code.

Trong blog này, nếu không nói gì thêm, chúng ta giả sử rằng các đạo hàm tồn tại. Tài liệu tham khảo chính của chương là Matrix calculus–Stanford

1 Đạo hàm của hàm trả về một số vô hướng

  • Đạo hàm bậc nhất (first-order gradient) hay viết gọn là đạo hàm (gradient) của một hàm số $f(\mathbf{x}): \mathbb{R}^n \rightarrow \mathbb{R}$ theo $\mathbf{x}$ được định nghĩa là:
\[\begin{equation} \label{eqn:grvector1} \nabla_{\mathbf{x}} f(\mathbf{x}) \triangleq \left[ \begin{matrix} \dfrac{\partial f(\mathbf{x})}{\partial x_1} \\\ \dfrac{\partial f(\mathbf{x})}{\partial x_2} \\\ \vdots \\\ \dfrac{\partial f(\mathbf{x})}{\partial x_n} \end{matrix} \right] \in \mathbb{R}^n, \end{equation}\]
  • Trong đó $\displaystyle\dfrac{\partial f(\mathbf{x})}{\partial x_i}$ là đạo hàm riêng của hàm số theo thành phần thứ $i$ của vector $\mathbf{x}$. Đạo hàm này được tính khi tất cả các biến, ngoài $x_i$, được giả sử là hằng số. Nếu không có thêm biến nào khác, $\nabla_{\mathbf{x}}f(\mathbf{x})$ thường được viết gọn là $\nabla f(\mathbf{x})$. Đạo hàm của hàm số này là một vector có cùng chiều với vector đang được lấy đạo hàm. Tức nếu vector được viết ở dạng cột thì đạo hàm cũng phải được viết ở dạng cột.
  • Đạo hàm bậc hai (second-order gradient) của hàm số trên còn được gọi là Hessian và được định nghĩa như sau, với $\mathbb{S}^n \in \mathbb{R}^{n \times n}$ là tập các ma trận vuông đối xứng bậc $n$.
\[\displaystyle \nabla^2 f(\mathbf{x}) \triangleq \begin{bmatrix} \frac{\partial^2 f(\mathbf{x})}{\partial x_1^2} & \frac{\partial^2 f(\mathbf{x})}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f(\mathbf{x})}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f(\mathbf{x})}{\partial x_2 \partial x_1} & \frac{\partial^2 f(\mathbf{x})}{\partial x_2^2} & \cdots & \frac{\partial^2 f(\mathbf{x})}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f(\mathbf{x})}{\partial x_n \partial x_1} & \frac{\partial^2 f(\mathbf{x})}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f(\mathbf{x})}{\partial x_n^2} \end{bmatrix} \in \mathbb{S}^n\]
  • Đạo hàm của một hàm số $f(\mathbf{X}): \mathbb{R}^{n \times m} \rightarrow \mathbb{R}$ theo ma trận $\mathbf{X}$ được định nghĩa là:
\[\nabla f(\mathbf{X}) = \begin{bmatrix} \frac{\partial f(\mathbf{X})}{\partial x_{11}} & \frac{\partial f(\mathbf{X})}{\partial x_{12}} & \cdots & \frac{\partial f(\mathbf{X})}{\partial x_{1m}} \\ \frac{\partial f(\mathbf{X})}{\partial x_{21}} & \frac{\partial f(\mathbf{X})}{\partial x_{22}} & \cdots & \frac{\partial f(\mathbf{X})}{\partial x_{2m}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f(\mathbf{X})}{\partial x_{n1}} & \frac{\partial f(\mathbf{X})}{\partial x_{n2}} & \cdots & \frac{\partial f(\mathbf{X})}{\partial x_{nm}} \end{bmatrix} \in \mathbb{R}^{n \times m}\]

anh

  • Cụ thể, để tính đạo hàm của một hàm $f: \mathbb{R}^{m\times n} \rightarrow \mathbb{R}$, ta tính đạo hàm riêng của hàm số đó theo từng thành phần của ma trận khi toàn bộ các thành phần khác được giả sử là hằng số. Tiếp theo, ta sắp xếp các đạo hàm riêng tính được theo đúng thứ tự trong ma trận.

  • Ví dụ: Xét hàm số $f: \mathbb{R}^2 \rightarrow \mathbb{R}$, $f(\mathbf{x}) = x_1 ^2 + 2x_1x_2 + \sin(x_1) + 2$. Đạo hàm bậc nhất theo $\mathbf{x}$ của hàm số đó là:

\[\nabla f(\mathbf{x}) = \begin{bmatrix} \frac{\partial f(\mathbf{x})}{\partial x_1} \\ \frac{\partial f(\mathbf{x})}{\partial x_2} \end{bmatrix} = \begin{bmatrix} 2x_1 + 2x_2 + \cos(x_1) \\ 2x_1 \end{bmatrix}\]
  • Đạo hàm bậc hai theo $\mathbf{x}$, hay Hessian là:
\[\nabla^2 f(\mathbf{x}) = \begin{bmatrix} \frac{\partial^2 f(\mathbf{x})}{\partial x_1^2} & \frac{\partial^2 f(\mathbf{x})}{\partial x_1 \partial x_2} \\ \frac{\partial^2 f(\mathbf{x})}{\partial x_2 \partial x_1} & \frac{\partial^2 f(\mathbf{x})}{\partial x_2^2} \end{bmatrix} = \begin{bmatrix} 2 - \sin(x_1) & 2 \\ 2 & 0 \end{bmatrix}.\]
  • Chú ý rằng Hessian luôn là một ma trận đối xứng. Bạn có thể dùng thư viện sympy trong python để tính đạo hàm, ví dụ dưới đây là tính đạo hàm bậc một với đầu vào là vector và đầu ra là số vô hướng:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

import sympy as sp

# Khai báo biến vector x
x1, x2 = sp.symbols('x1 x2')
x = sp.Matrix([x1, x2])

# Định nghĩa hàm cần tính đạo hàm
f = x1**2 + 2*x1*x2 + sp.sin(x1) + 2

# Tính gradient (đạo hàm theo từng biến)
gradient = [sp.diff(f, xi) for xi in x]

# Hiển thị kết quả
print("Hàm:", f)
print("Gradient:", gradient)
  • Ví dụ dưới đây là đạo hàm bậc hai của hàm trên:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

import sympy as sp

# Khai báo các biến
x1, x2 = sp.symbols('x1 x2')
x = sp.Matrix([x1, x2])

# Định nghĩa hàm cần tính đạo hàm
f = x1**2 + 2*x1*x2 + sp.sin(x1) + 2

# Tính gradient (đạo hàm bậc 1)
gradient = sp.Matrix([sp.diff(f, xi) for xi in x])  # Gradient là vector

# Tính Hessian (đạo hàm bậc 2)
hessian = gradient.jacobian(x)  # Hessian là ma trận

# Hiển thị kết quả
print("Hàm:", f)
print("Gradient:", gradient)
print("Hessian:")
sp.pprint(hessian)  # In đẹp hơn
  • Dưới đây là ví dụ nếu như đầu vào là ma trận và đầu ra là số vô hướng:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

import sympy as sp

# Khai báo ma trận X (kích thước m x n)
m, n = 2, 2  # Ví dụ: ma trận 2x2
X = sp.MatrixSymbol('X', m, n)  # Tạo ma trận ký hiệu
X_mat = sp.Matrix(m, n, lambda i, j: sp.Symbol(f'X{i+1}{j+1}'))  # Ma trận cụ thể

# Định nghĩa hàm f (hàm số vô hướng)
f = sp.trace(X_mat.T * X_mat) + sp.det(X_mat)  # Ví dụ: f = tr(X^T X) + det(X)

# Tính gradient (đạo hàm bậc 1 theo từng phần tử của X)
gradient = sp.Matrix([sp.diff(f, X_mat[i, j]) for i in range(m) for j in range(n)])
gradient = gradient.reshape(m, n)  # Chuyển về dạng ma trận

# Hiển thị kết quả
print("Hàm f:")
sp.pprint(f)

print("\nGradient (đạo hàm bậc 1):")
sp.pprint(gradient)

2 Đạo hàm của hàm trả về một vector

  • Những hàm số trả về một vector, hoặc gọn hơn hàm trả về vector được gọi là vector-valued function trong tiếng Anh.
  • Xét một hàm trả về vector với đầu vào là một số thực $v(x): \mathbb{R} \rightarrow \mathbb{R}^n $:
\[v(x) = \begin{bmatrix} v_1(x) \\ v_2(x) \\ \vdots \\ v_n(x) \end{bmatrix}.\]
  • Đạo hàm của hàm số này theo $x$ là một vector hàng như sau:
\[\nabla v(x) \triangleq \begin{bmatrix} \frac{\partial v_1(x)}{\partial x} & \frac{\partial v_2(x)}{\partial x} & \cdots & \frac{\partial v_n(x)}{\partial x} \end{bmatrix}.\]
  • Đạo hàm bậc hai của hàm số này có dạng:
\[\nabla^2 v(x) \triangleq \begin{bmatrix} \frac{\partial^2 v_1(x)}{\partial x^2} & \frac{\partial^2 v_2(x)}{\partial x^2} & \cdots & \frac{\partial^2 v_n(x)}{\partial x^2} \end{bmatrix}.\]
  • Ví dụ: Cho một vector $\mathbf{a} \in \mathbb{R}^n$ và một hàm số vector-valued $v(x) = x\mathbf{a}$, đạo hàm bậc nhất và Hession của nó lần lượt là:
\[\begin{equation} \nabla v(x) = \mathbf{a}^T, ~~~ \nabla^2 v(x) = \mathbf{0} \in \mathbb{R}^{1\times n}. \end{equation}\]
  • Dưới đây là ví dụ python về tính đạo hàm bậc nhất và đạo hàm bậc hai của hàm trả về một vector:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

from sympy import symbols, diff, Matrix

# Định nghĩa biến đầu vào
x = symbols('x')

# Định nghĩa hàm đầu vào (trả về một vector)
def f(x):
    return Matrix([x**2, x**3, x + 1])

# Tính đạo hàm bậc nhất
vector_output = f(x)
jacobian = vector_output.jacobian([x])

# Tính đạo hàm bậc hai
second_derivative = jacobian.applyfunc(lambda expr: diff(expr, x))

print("Jacobian bậc 1 của hàm f(x) là:")
print(jacobian)

print("\nJacobian bậc 2 của hàm f(x) là:")
print(second_derivative)
  • Xét một hàm trả về vector với đầu vào là một vector $h(\mathbf{x}):\mathbb{R}^k \rightarrow \mathbb{R}^n$, đạo hàm bậc nhất của nó là:
\[\nabla h(\mathbf{x}) \triangleq \begin{bmatrix} \frac{\partial h_1(\mathbf{x})}{\partial x_1} & \frac{\partial h_2(\mathbf{x})}{\partial x_1} & \cdots & \frac{\partial h_n(\mathbf{x})}{\partial x_1} \\ \frac{\partial h_1(\mathbf{x})}{\partial x_2} & \frac{\partial h_2(\mathbf{x})}{\partial x_2} & \cdots & \frac{\partial h_n(\mathbf{x})}{\partial x_2} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial h_1(\mathbf{x})}{\partial x_k} & \frac{\partial h_2(\mathbf{x})}{\partial x_k} & \cdots & \frac{\partial h_n(\mathbf{x})}{\partial x_k} \end{bmatrix} = \begin{bmatrix} \nabla h_1(\mathbf{x}) & \nabla h_2(\mathbf{x}) & \cdots & \nabla h_n(\mathbf{x}) \end{bmatrix} \in \mathbb{R}^{k \times n}.\]

anh

  • Đây là code tính đạo hàm bậc nhất của hàm số trên:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

from sympy import symbols, Matrix, diff

# Định nghĩa các biến đầu vào (vector đầu vào)
x1, x2 = symbols('x1 x2')  # Vector đầu vào có 2 biến
X = Matrix([x1, x2])       # Vector đầu vào

# Định nghĩa hàm đầu vào (vector đầu ra)
def f(X):
    x1, x2 = X[0], X[1]
    return Matrix([x1**2 + x2, x1 * x2, x2**3])

# Tính đạo hàm bậc nhất (Jacobian)
vector_output = f(X)
jacobian = vector_output.jacobian(X)

print("Jacobian của hàm f(X) là:")
print(jacobian)
  • Đạo hàm bậc hai của hàm số trên là một mảng ba chiều, chúng ta sẽ không nhắc đến ở đây.
  • Trước khi đến phần tính đạo hàm của các hàm số thường gặp, chúng ta cần biết hai tính chất quan trọng khá giống với đạo hàm của hàm một biến.

3. Tính chất quan trọng của đạo hàm

3.1 Quy tắc tích (Product rule)

  • Để cho tổng quát, ta giả sử biến đầu vào là một ma trận. Giả sử rằng các hàm số có chiều phù hợp để các phép nhân thực hiện được. Ta có:
\[\begin{equation} \label{eqn:productrules} \nabla\left( f(\mathbf{X})^Tg(\mathbf{X}) \right) = \left(\nabla f(\mathbf{X})\right) g(\mathbf{X}) + \left(\nabla g(\mathbf{X})\right) f(\mathbf{X}). \end{equation}\]
  • Biểu thức này giống như biểu thức chúng ta đã quen thuộc:
\[\begin{equation*} \left(f(x)g(x)\right)' = f'(x)g(x) + g'(x)f(x). \end{equation*}\]
  • Chú ý rằng với tích của vector và ma trận, ta không được sử dụng tính chất giao hoán.

3.2 Quy tắc chuỗi (Chain rule)

  • Khi có các hàm hợp thì:
\[\begin{equation} \label{eqn:chainrules} \nabla_{\mathbf{X}} g(f(\mathbf{X})) = (\nabla_{\mathbf{X}} f) (\nabla_{f}g). \end{equation}\]
  • Quy tắc này cũng giống với quy tắc trong hàm một biến:
\[\begin{equation*} (g(f(x)))' = f'(x)g'(f). \end{equation*}\]
  • Một lưu ý nhỏ nhưng quan trọng khi làm việc với tích các ma trận là sự phù hợp về kích thước của các ma trận trong tích.

4. Đạo hàm của các hàm số thường gặp

4.1 $f(\mathbf{x}) = \mathbf{a}^T\mathbf{x}$

  • Giả sử $\mathbf{a}, \mathbf{x} \in \mathbb{R}^n$, ta viết lại $f(\mathbf{x}) = \mathbf{a}^T\mathbf{x} = a_1 x_1 + a_2 x_2 + \dots + a_nx_n$.
  • Có thể nhận thấy rằng $\dfrac{\partial f(\mathbf{x})}{\partial x_i} = a_i, ~\forall i = 1, 2\dots, n$
  • Vậy, $ \nabla (\mathbf{a}^T \mathbf{x}) = \begin{bmatrix} a_1 a_2 \dots & a_n \end{bmatrix}^T = \mathbf{a} $. Ngoài ra, vì $\mathbf{a}^T\mathbf{x} = \mathbf{x}^T\mathbf{a}$ nên $\nabla_{\mathbf{x}} (\mathbf{x}^T\mathbf{a}) = \mathbf{a}$.

4.2 $f(\mathbf{x}) = \mathbf{\mathbf{A}\mathbf{x}}$

  • Đây là một hàm trả về vector $f: \mathbb{R}^n \rightarrow \mathbb{R}^{m} $ với $\mathbf{x} \in \mathbb{R}^n, \mathbf{A} \in \mathbb{R}^{m\times n}$. Giả sử $\mathbf{a}_i$ là hàng thứ $i$ của ma trận $\mathbf{A}$. Ta có:
\[\mathbf{Ax} = \begin{bmatrix} a_1 \mathbf{x} \\ a_2 \mathbf{x} \\ \vdots \\ a_m \mathbf{x} \end{bmatrix}\]
  • Từ định nghĩa đạo hàm vởi hàm trả về vector với đầu vào là một vector và công thức gradient của $\mathbf{a}_i\mathbf{x}$, có thể suy ra:
\[\nabla_{\mathbf{x}} ( \mathbf{Ax}) = \begin{bmatrix} \mathbf{a}_1^T & \mathbf{a}_2^T & \dots & \mathbf{a}_m^T \end{bmatrix} = \mathbf{A}^T\]
  • Từ đây suy ra đạo hàm của hàm số $f(\mathbf{x}) = \mathbf{x} = \mathbf{I\mathbf{x}}$ là:
\[\nabla \mathbf{x} = \mathbf{I}\]

2.4.3 $f(\mathbf{x}) = \mathbf{x}^T\mathbf{A} \mathbf{x}$

Với $\mathbf{x} \in \mathbb{R}^n, \mathbf{A} \in \mathbb{R}^{n\times n}$, áp dụng quy tắc tích ta có:

\[\begin{eqnarray} \nonumber \nabla f(\mathbf{x}) &=& \nabla \left(\left(\mathbf{x}^T\right) \left(\mathbf{Ax}\right)\right) \\\ \nonumber &=& \left(\nabla (\mathbf{x})\right) \mathbf{Ax} + \left(\nabla (\mathbf{Ax})\right)\mathbf{x} \\\ \nonumber & = & \mathbf{IAx} + \mathbf{A}^T\mathbf{x} \\\ \label{eqn:gdxTAx} & = & (\mathbf{A} + \mathbf{A}^T)\mathbf{x}. \end{eqnarray}\]

  • Từ phương trình trên và $\nabla_{\mathbf{x}} ( \mathbf{Ax}) = \begin{bmatrix} \mathbf{a}_1^T & \mathbf{a}_2^T & \dots & \mathbf{a}_m^T \end{bmatrix} = \mathbf{A}^T$, ta có thể suy ra $\nabla^2 \mathbf{x}^T \mathbf{A} \mathbf{x} = \mathbf{A}^T + \mathbf{A}$.

  • Nếu $\mathbf{A}$ là một ma trận đối xứng, ta có:

\[\nabla \mathbf{x}^T\mathbf{A}\mathbf{x} = 2\mathbf{Ax}, \nabla^2 \mathbf{x}^T\mathbf{Ax} = 2\mathbf{A}.\]
  • Nếu $\mathbf{A}$ là ma trận đơn vị, tức $f(\mathbf{x}) = \mathbf{x}^T\mathbf{Ix} = \mathbf{x}^T\mathbf{x} = |\mathbf{x}|_2^2$, ta có:
\[\begin{equation} \nabla \|\mathbf{x}\|_2^2 = 2\mathbf{x},~~~ \nabla^2 \|\mathbf{x}\|_2^2 = 2\mathbf{I}. \end{equation}\]

2.4.4 $f(\mathbf{x}) = |\mathbf{Ax} - \mathbf{b}|_2^2 $

  • Có hai cách tính gradient của hàm số này:
  • Cách 1: Trước hết, biến đổi
\[\begin{eqnarray} \nonumber f(\mathbf{x}) &=& \|\mathbf{Ax} - \mathbf{b}\|_2^2 = (\mathbf{Ax} - \mathbf{b})^T(\mathbf{Ax} - \mathbf{b}) = (\mathbf{x}^T\mathbf{A}^T - \mathbf{b}^T) (\mathbf{Ax} - \mathbf{b}) \\\ \nonumber &=& \mathbf{x}^T\mathbf{A}^T\mathbf{Ax} - 2 \mathbf{b}^T\mathbf{Ax} + \mathbf{b}^T\mathbf{b}. \end{eqnarray}\]
  • Lấy đạo hàm cho từng số hạng rồi cộng lại ta có:
\[\begin{equation*} \nabla \|\mathbf{Ax} - \mathbf{b}\|_2^2 = 2\mathbf{A}^T\mathbf{A}\mathbf{x} - 2\mathbf{A}^T\mathbf{b} = 2\mathbf{A}^T(\mathbf{Ax} - \mathbf{b}). \end{equation*}\]

  • Cách 2: Sử dụng $\nabla (\mathbf{Ax} - \mathbf{b}) = \mathbf{A}^T$ và $\nabla |\mathbf{x}|_2^2 = 2\mathbf{x}$ và quy tắc chuỗi, ta cũng sẽ thu được kết quả tương tự.

  • Bảng dưới đây bao gồm đạo hàm của các hàm số thường gặp với biến là vector hoặc ma trận:

anh

5. Kiểm tra đạo hàm

  • Việc tính đạo hàm của hàm nhiều biến thông thường khá phức tạp và rất dễ mắc lỗi. Trong thực nghiệm, có một cách để kiểm tra liệu đạo hàm tính được có chính xác không. Cách này dựa trên định nghĩa của đạo hàm cho hàm một biến.

5.1 Xấp xỉ đạo hàm của hàm một biến

  • Theo định nghĩa:
\[\begin{equation} \label{eqn:grdef1} f'(x) = \lim_{\varepsilon \rightarrow 0}\frac{f(x + \varepsilon) - f(x)}{\varepsilon}. \end{equation}\]
  • Trên máy tính, ta có thể chọn $\varepsilon$ rất nhỏ, ví dụ $10^{-6}$, rồi xấp xỉ đạo hàm này bởi:
\[\begin{equation} f'(x) \approx \lim_{\varepsilon \rightarrow 0}\frac{f(x + \varepsilon) - f(x)}{\varepsilon}. \end{equation}\]
  • Trên thực tế, công thức xấp xỉ đạo hàm hai phía thường được sử dụng:
\[\begin{equation} \label{eqn:grdef2} f'(x) \approx \frac{f(x + \varepsilon) - f(x - \varepsilon)}{2\varepsilon}. \end{equation}\]
  • Cách tính này được gọi là numerical gradient. Biểu thức trên được sử dụng rộng rãi hơn để tính numerical gradient. Có hai cách giải thích cho vấn đề này.

Bằng giải tích

  • Sử dụng khai triển Taylor với $\varepsilon$ rất nhỏ, ta có hai xấp xỉ sau:
\[\begin{eqnarray} f(x + \varepsilon) &\approx& f(x) + f'(x)\varepsilon + \frac{f"(x)}{2} \varepsilon^2 + \frac{f^{(3)}}{6}\varepsilon^3 + \dots \\ f(x - \varepsilon) &\approx& f(x) - f'(x)\varepsilon + \frac{f"(x)}{2} \varepsilon^2 - \frac{f^{(3)}}{6}\varepsilon^3 + \dots \end{eqnarray}\]
  • Từ đó ta có:
\[\begin{eqnarray} \label{eqn:numgrdef1} \frac{f(x + \varepsilon) - f(x)}{\varepsilon} &\approx& f'(x) + \frac{f"(x)}{2}\varepsilon + \dots = f'(x) + O(\varepsilon). \\ \label{eqn:numgrdef2} \frac{f(x + \varepsilon) - f(x - \varepsilon)}{2\varepsilon} &\approx& f'(x) + \frac{f^{(3)}(x)}{6}\varepsilon^2 + \dots = f'(x) + O(\varepsilon^2). \end{eqnarray}\]
  • Trong đó $O()$ là {Big O notation}. Từ đó, nếu xấp xỉ đạo hàm bằng công thức đầu tiên, sai số sẽ là $O(\varepsilon)$. Trong khi đó, nếu xấp xỉ đạo hàm bằng công thức thứ hai, sai số sẽ là $O(\varepsilon^2)$. Khi $\varepsilon$ rất nhỏ, $O(\varepsilon^2) \ll O(\varepsilon)$, tức cách đánh giá sử dụng công thức dưới có sai số nhỏ hơn, và vì vậy nó được sử dụng phổ biến hơn.

Bằng hình học

anh

  • Quan sát hình trên, vector màu đỏ là đạo hàm chính xác của hàm số tại điểm có hoành độ bằng $x_0$. Vector màu xanh lam và xanh lục lần lượt thể hiện cách xấp xỉ đạo hàm phía phải và phía trái. Vector màu nâu thể hiện cách xấp xỉ đạo hàm hai phía. Trong ba vector xấp xỉ đó, vector xấp xỉ hai phía màu nâu là gần với vector đỏ nhất nếu xét theo hướng.
  • Sự khác biệt giữa các cách xấp xỉ còn lớn hơn nữa nếu tại điểm $x$, hàm số bị bẻ cong mạnh hơn. Khi đó, xấp xỉ trái và phải sẽ khác nhau rất nhiều. Xấp xỉ hai bên sẽ ổn định hơn.
  • Từ đó ta thấy rằng xấp xỉ đạo hàm hai phía là xấp xỉ tốt hơn

    6. Tổng Kết

  • Học giải tích ma trận giúp ta hiểu được tại sao khi đạo hàm trên hàm mất mát lại ra được các công thức như trên trong các thuật toán học máy. Nếu chưa hiểu rõ thì hãy đọc lại một lần nữa vì phần này khá quan trọng. Để biết thêm chi tiết, vui lòng tham khảo Chương 2: Giải tích ma trận trong sách Machine Learning Cơ Bản
Machine Learning
linear
This post is licensed under CC BY 4.0 by the author.