Hồi qui Ridge và Lasso
Mục tiêu của bài viết này là giúp chúng ta hiểu về mô hình hồi qui Ridge và mô hình hồi qui Lasso. Giả định bạn đang xây dựng mô hình hồi qui tuyến tính nhưng thật không may mắn, mô hình của bạn gặp hiện tượng quá khớp (overfitting). Khi đó bạn có thể nghĩ đến một số ý tưởng:
- Giảm bớt số lượng biến đầu vào.
- Loại bỏ outliers.
- Xử lý các trường hợp dữ liệu bị khuyết.
- Thu thập thêm dữ liệu huấn luyện.
- Thay đổi lớp mô hình.
…
Có khá nhiều ý tưởng cho bạn thử nghiệm, một trong số chúng có thể giúp bạn khắc phục hiện tượng quá khớp. Đa phần các kĩ thuật đều liệu quan tới xử lý dữ liệu đầu vào một cách thủ công và cần phải cân nhắc trước khi đưa ra một quyết định thay đổi dữ liệu đầu vào. Nhưng có một phương pháp khá hiệu quả giúp khắc phục tức thời hiện tượng quá khớp mà không đòi hỏi chúng ta phải thay đổi dữ liệu. Đó chính là hồi qui Ridge và Lasso mà chúng ta sẽ tìm hiểu trong bài viết này. Vậy thì Ridge và Lasso là những mô hình như thế nào ? Vì sao chúng lại khắc phục được hiện tượng quá khớp ? Một cách khách quan, Ridge và Lasso là những biến thể của hồi qui tuyến tính mà ở đó chúng ta thay đổi hàm mất mát MSE để kiểm soát độ lớn của tham số huấn luyện nhằm giảm thiểu hiện tượng quá khớp trong các bài toán dự báo của học có giám sát. Qua bài viết này bạn sẽ được tìm hiểu:
- Lý thuyết đằng sau hai lớp mô hình là gì ?
- Lời giải cho bài toán tối ưu.
- Đặc điểm của nghiệm trả về.
- Cách lựa chọn hệ số nhân $\alpha$ của thành phần điều chuẩn cho những mô hình này.
1. Hồi qui Ridge
Tính tổng quát của mô hình
Một mục tiêu tiên quyết để có thể áp dụng được mô hình vào thực tiến đó là chúng ta cần giảm thiểu hiện tượng quá khớp. Để thực hiện được mục tiêu đó, mô hình được huấn luyện được kì vọng sẽ nắm bắt được qui luật tổng quát từ tập huấn luyện (train dataset) mà qui luật đó phải đúng trên những dữ liệu mới mà nó chưa được học. Thông thường tập dữ liệu mới đó được gọi là tập kiểm tra (test dataset). Đây là một tập dữ liệu độc lập được sử dụng để đánh giá mô hình.
Bài toán hồi qui tuyến tính
Giả định dữ liệu đầu vào bao gồm $N$ quan sát là những cặp các biến đầu vào và biến mục tiêu $(\mathbf{x}_1, y_1), (\mathbf{x}_2, y_2),…,(\mathbf{x}_N, y_N)$. Quá trình hồi qui mô hình sẽ tìm kiếm một véc tơ hệ số ước lượng $\mathbf{w} = [w_0,w_1,…,w_p]$ sao cho tối thiểu hoá hàm mất mát dạng MSE:
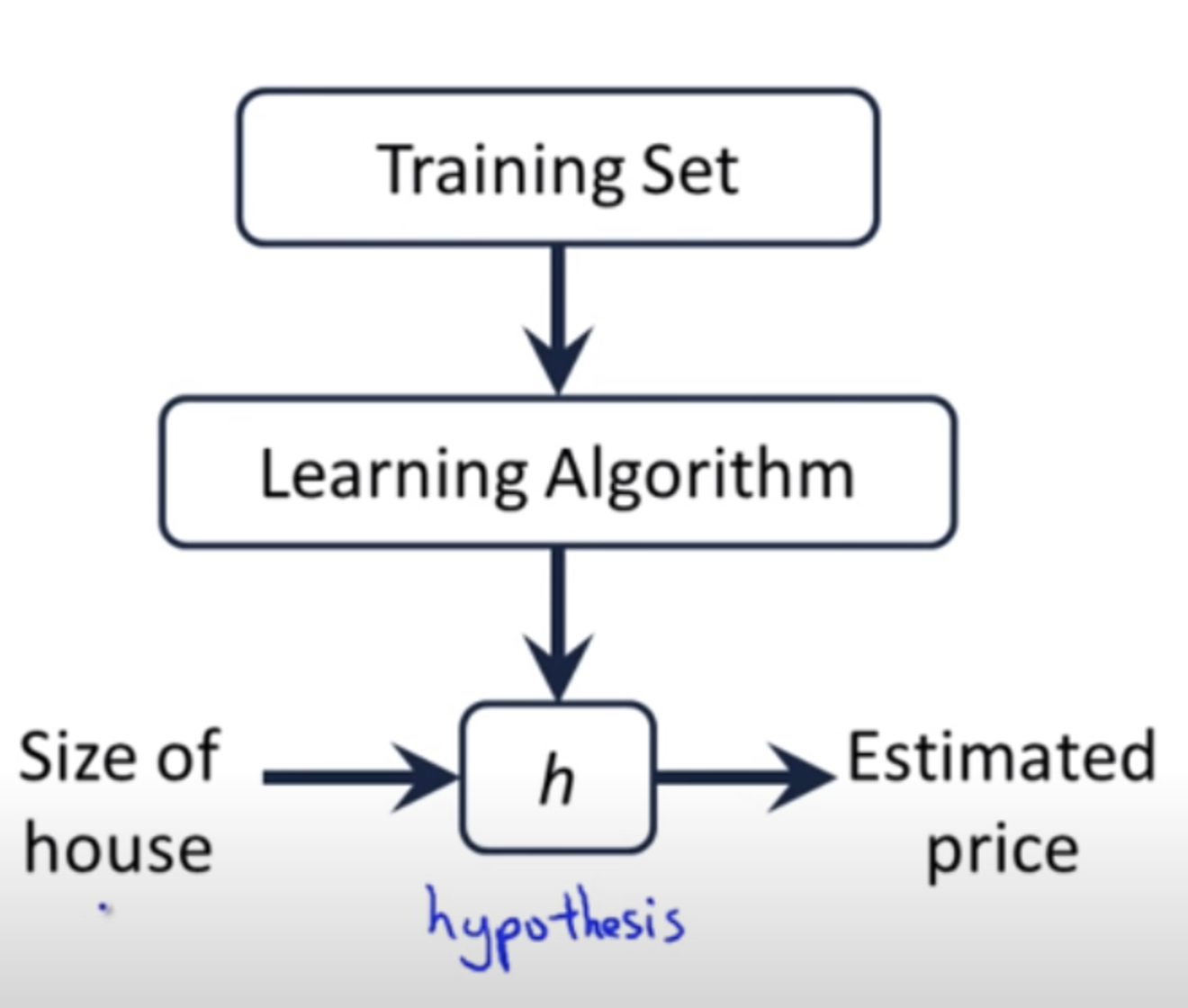
\[\mathcal{L}(\mathbf{w}) = \frac{1}{N} \sum_{i=1}^{N} (y_i - \mathbf{w}^\top \mathbf{x}_i)^2 = \frac{1}{N} \| \bar{\mathbf{X}} \mathbf{w} - \bar{\mathbf{y}} \|_2^2\]Nhắc lại một chút về khái niệm hàm mất mát. Trong các mô hình học có giám sát của machine learning, từ dữ liệu đầu vào, thông qua phương pháp học tập (learning algorithm), chúng ta sẽ đặt ra một hàm giả thuyết $h$ (hypothesis function) mô tả mối quan hệ dữ liệu giữa biến đầu vào và biến mục tiêu.
Hình trên cho thấy từ một quan sát đầu vào $\mathbf{x}_i$, sau khi đưa vào hàm gỉa thuyết $h$ chúng ta thu được giá trị dự báo $\hat{y}$ ở đầu ra. Chữ $h$ của tên hàm thể hiện cho từ hypothesis có nghĩa là giả thuyết, đây là một khái niệm đã tồn tại lâu năm trong thống kê. Để mô hình càng chuẩn xác thì sai số giữa giá trị dự báo $\hat{y}$ và ground truth $y$ càng phải nhỏ. Vậy làm thế nào để đo lường được mức độ nhỏ của sai số giữa $\hat{y}$ và $y$ ? Các thuật toán học có giám sát trong machine learning sẽ sử dụng hàm mất mát để lượng hoá sai số này.
Hàm mất mát cũng chính là mục tiêu tối ưu khi huấn luyện mô hình. Dữ liệu đầu vào $\mathbf{X}$ và $y$ được xem như là cố định và biến số của bài toán tối ưu chính là các giá trị trong véc tơ $\mathbf{w}$.
Giá trị hàm mất mát MSE chính là trung bình của tổng bình phương phần dư. Phần dư chính là chênh lệch giữa giá trị thực tế và giá trị dự báo. Tối thiểu hoá hàm mất mát nhằm mục đích làm cho giá trị dự báo ít chênh lệch so với giá trị thực tế, giá trị thực tế còn được gọi là ground truth. Trước khi huấn luyện mô hình chúng ta chưa thực sự biết véc tơ hệ số $\mathbf{w}$ là gì. Chúng ta chỉ có thể đặt ra một giả thuyết về dạng hàm dự báo (trong trường hợp này là phương trình dạng tuyến tính) và các hệ số hồi qui tương ứng. Chính vì vậy mục đích của tối thiểu hoá hàm mất mát là để tìm ra tham số $\mathbf{w}$ phù hợp nhất mô tả một cách khái quát quan hệ dữ liệu giữa biến đầu vào $\mathbf{X}$ với biến mục tiêu $\mathbf{y}$ trên tập huấn luyện.
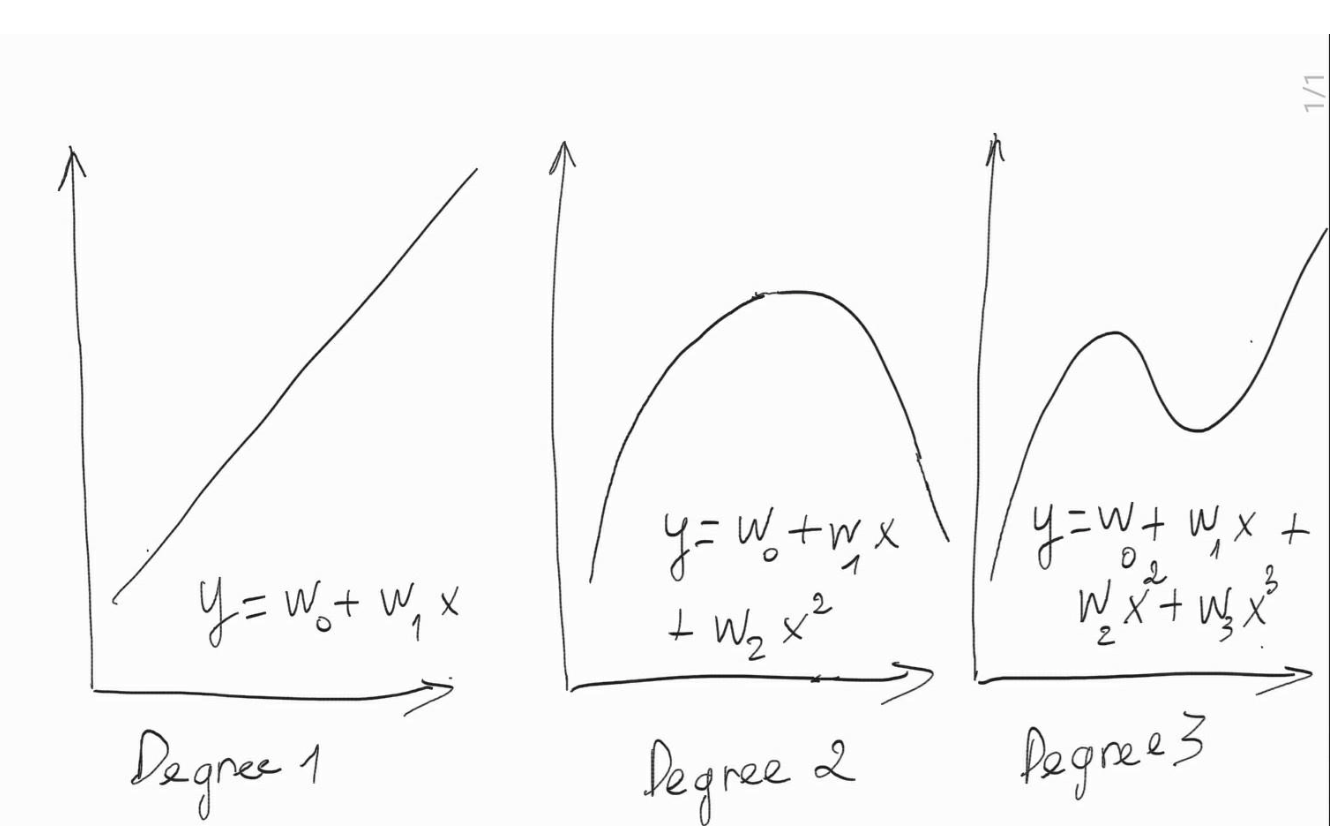
Tuy nhiên mối quan hệ này nhiều khi không mô tả được qui luật khái quát của dữ liệu nên dẫn tới hiện tượng quá khớp. Một trong những nguyên nhân dẫn tới sự không khái quát của mô hình đó là do mô hình quá phức tạp. Mức độ phức tạp càng cao khi độ lớn của các hệ số trong mô hình hồi qui ở những bậc cao có xu hướng lớn như phân tích trong hình bên dưới:
Hình trên thể hiện mức độ phức tạp của mô hình theo sự thay đổi của bậc. Phương trình có độ phức tạp lớn nhất là phương trình bậc $3$: $y = w_0 + w_1x + w_2x^2 + w_3x^3$. Trong chương trình THPT chúng ta biết rằng phương trình bậc $3$ thông thường sẽ có $2$ điểm uốn và độ phức tạp lớn hơn bậc hai chỉ có $1$ điểm uốn. Khi $w_3 \to 0$ thì phương trình bậc $3$ hội tụ về phương trình bậc $2$: $y = w_0 + w_1x + w_2x^2$, lúc này phương trình là một đường cong dạng parbol và có độ phức tạp giảm. Tiếp tục kiểm soát độ lớn để $w_2 \to 0$ trong phương trình bậc $2$ ta sẽ thu được một đường thẳng tuyến tính dạng $y = w_0 + w_1x$ có độ phức tạp thấp nhất.
Như vậy kiểm soát độ lớn của hệ số ước lượng, đặc biệt là với bậc cao, sẽ giúp giảm bớt mức độ phức tạp của mô hình và thông qua đó khắc phục hiện tượng quá khớp. Vậy làm cách nào để kiểm soát chúng, cùng tìm hiểu chương bên dưới.
Sự thay đổi của hàm mất mát trong hồi qui Ridge
Hàm mất mát trong hồi qui Ridge sẽ có sự thay đổi so với hồi qui tuyến tính đó là thành phần điều chuẩn (regularization term) được cộng thêm vào hàm mất mát như sau:
\[\mathcal{L}(\mathbf{w}) = \frac{1}{N} \| \bar{\mathbf{X}} \mathbf{w} - \bar{\mathbf{y}} \|_2^2 + \alpha \| \mathbf{w} \|_2^2 \\ \quad = \frac{1}{N} \| \bar{\mathbf{X}} \mathbf{w} - \bar{\mathbf{y}} \|_2^2 + \underbrace{\alpha R(\mathbf{w})}_{\text{regularization term}}\]Trong phương trình trên thì $\alpha \geq 0$. $\frac{1}{N} || \bar{\mathbf{X}} \mathbf{w} - \bar{\mathbf{y}} ||_2^2$ chính là tổng bình phương phần dư và $ \alpha || \mathbf{w} ||_2^2$ đại diện cho thành phần điều chuẩn.
Bài toán tối ưu hàm mất mát của hồi qui Ridge về bản chất là tối ưu song song hai thành phần bao gồm tổng bình phương phần dư và thành phần điều chuẩn. Hệ số $\alpha$ có tác dụng điều chỉnh độ lớn của thành phần điều chuẩn tác động lên hàm mất mát.
Trường hợp $\alpha = 0$, thành phần điều chuẩn bị tiêu giảm và chúng ta quay trở về bài toán hồi qui tuyến tính.
Trường hợp $\alpha$ nhỏ thì vai trò của thành phần điều chuẩn trở nên ít quan trọng. Mức độ kiểm soát quá khớp của mô hình sẽ trở nên kém hơn.
Trường hợp $\alpha$ lớn chúng ta muốn gia tăng mức độ kiểm soát lên độ lớn của các hệ số ước lượng và qua đó giảm bớt hiện tượng qúa khớp.
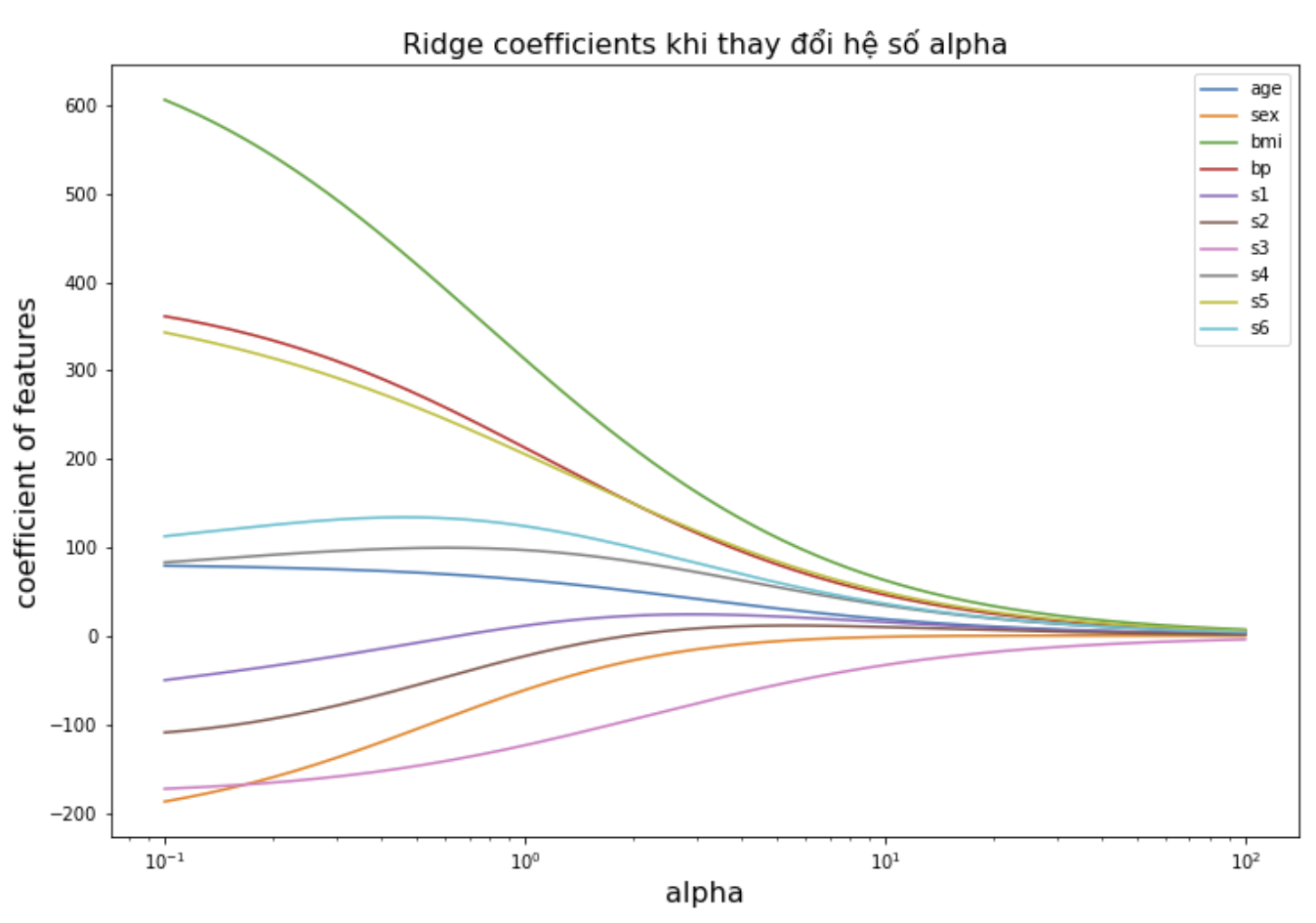
Khi tăng dần hệ số $\alpha$ thì hồi qui Ridge sẽ có xu hướng thu hẹp hệ số ước lượng từ mô hình. Chúng ta sẽ thấy rõ thông qua ví dụ mẫu bên dưới.
Import thư viện và đọc dữ liệu đầu vào
Bộ dữ liệu đầu vào được sử dụng cho ví dụ này là diabetes. Thông tin về bộ dữ liệu này bạn đọc có thể tham khảo tại sklearn diabetes dataset.
Mục tiêu của mô hình là từ $10$ biến đầu vào là những thông tin liên quan tới người bệnh bao gồm age, sex, body mass index, average blood pressure và $6$ chỉ số blood serum. Chúng ta sẽ dự báo biến mục tiêu là một thước đo định lượng sự tiến triển của bệnh sau $1$ năm điều trị.
1
2
3
4
5
6
7
8
9
10
11
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.linear_model import Ridge
from sklearn.datasets import load_diabetes
X,y = load_diabetes(return_X_y=True)
features = load_diabetes()['feature_names']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import numpy as np
import matplotlib.pyplot as plt
# Thay đổi alphas từ 1 --> 100
n_alphas = 200
alphas = 1/np.logspace(1, -2, n_alphas)
coefs = []
# Huấn luyện model khi alpha thay đổi.
for a in alphas:
ridge = Ridge(alpha=a, fit_intercept=False)
ridge.fit(X_train, y_train)
coefs.append(ridge.coef_)
# Hiển thị kết quả mô hình cho các hệ số alpha
plt.figure(figsize= (12, 8))
ax = plt.gca()
ax.plot(alphas, coefs)
ax.set_xscale('log')
ax.set_xlim(ax.get_xlim())
plt.xlabel('alpha', fontsize=16)
plt.ylabel('coefficient of features', fontsize=16)
plt.legend(features)
plt.title('Ridge coefficients khi thay đổi hệ số alpha', fontsize=16)
plt.axis('tight')
plt.show()