Hồi Quy Tuyến Tính

---

Phương trình hồi qui tuyến tính có rất nhiều ứng dụng trong thực tiễn và là một trong những lớp mô hình đặc biệt quan trọng trong machine learning. Chúng ta sẽ không thể kể hết được ứng dụng của nó trong một vài dòng. Nhưng chúng ta có thể xét đến một vài ví dụ tiêu biểu và gần gũi với mọi người, chẳng hạn như các bạn thường được nghe các dự báo trên truyền hình về chỉ số lạm phát, tốc độ tăng trưởng GDP của quốc gia hay dự báo về nhu cầu thị trường của một doanh nghiệp để chuẩn bị kế hoạch sản suất kinh doanh. Trong tài chính chúng ta có thể dự báo giá chứng khoán và các chỉ số tài chính dựa trên hồi qui tuyến tính.

1. Giới thiệu

• Giả sử ta cần làm bài toán như sau: một căn nhà rộng $x_1$ $m^2$, có $x_2$ phòng ngủ và cách trung tâm thành phố $x_3$ km có giá là bao nhiêu. Giả sử chúng ta đã có số liệu thống kê từ $1000$ căn nhà trong thành phố đó, liệu rằng khi có một căn nhà mới với các thông số về diện tích, số phòng ngủ và khoảng cách tới trung tâm, chúng ta có thể dự đoán được giá của căn nhà đó không ? Nếu có thì hàm dự đoán $y = f(\mathbf{x})$ sẽ có dạng như nào. Ở đây $\mathbf{x} = [x_1,x_2,x_3]$ là vector hàng chứa thông tin input, $y$ là một số vô hướng (scalar) biểu diễn ouput (tức giá của căn nhà trong ví dụ này).

• Lưu ý về ký hiệu toán học: trong các bài viết của tôi, các số vô hướng được biểu diễn bởi các chữ cái viết ở dạng không in đậm, có thể viết hoa, ví dụ $x_1, N, y,k$. Các vector được biểu diễn bằng các chữ cái thường in đậm, ví dụ $\mathbf{y}, \mathbf{x}_1$. Các ma trận được biểu diễn bởi các chữ viết hoa in đậm, ví dụ $\mathbf{X}, \mathbf{Y}, \mathbf{W}$.
• Một cách đơn giản nhất, chúng ta có thể thấy rằng: i) diện tích nhà càng lớn thì giá nhà càng cao; ii) số lượng phòng ngủ càng lớn thì giá nhà càng cao; iii) càng xa trung tâm thì giá nhà càng giảm. Một hàm số đơn giản nhất có thể mô tả mối quan hệ giữa giá nhà và $3$ đại lượng đầu vào là:

\[y \approx f(\mathbf{x}) = \hat{y}\] \[f(\mathbf{x}) = w_1 x_1 + w_2 x_2 + w_3 x_3 + w_0 \tag{1}\]

• Trong đó, $w_1,w_2,w_3,w_0$ là các hằng số, $w_0$ còn được gọi là bias. Mối quan hệ $y \approx f(\mathbf{x})$ bên trên là một mối quan hệ tuyến tính (linear). Bài toán chúng ta đang làm là một bài toán thuộc loại regression. Bài toán đi tìm các hệ số tối ưu ${w_1,w_2,w_3,w_0}$ chính vì vậy được gọi là bài toán Linear Regression.

• Chú ý 1: $y$ là giá trị thực của outcome (dựa trên số liệu thống kê chúng ta có trong tập training data), trong khi $\hat{y}$ là giá trị mà mô hình Linear Regression dự đoán được. Nhìn chung, $y$ và $\hat{y}$ là hai giá trị khác nhau do có sai số mô hình, tuy nhiên, chúng ta mong muốn rằng sự khác nhau này rất nhỏ.

• Chú ý 2: Linear hay tuyến tính hiểu một cách đơn giản là thẳng, phẳng. Trong không gian hai chiều, một hàm số được gọi là tuyến tính nếu đồ thị của nó có dạng một đường thẳng. Trong không gian ba chiều, một hàm số được goi là tuyến tính nếu đồ thị của nó có dạng một mặt phẳng. Trong không gian nhiều hơn 3 chiều, khái niệm mặt phẳng không còn phù hợp nữa, thay vào đó, một khái niệm khác ra đời được gọi là siêu mặt phẳng (hyperplane). Các hàm số tuyến tính là các hàm đơn giản nhất, vì chúng thuận tiện trong việc hình dung và tính toán. Chúng ta sẽ được thấy trong các bài viết sau, tuyến tính rất quan trọng và hữu ích trong các bài toán Machine Learning. Kinh nghiệm cá nhân tôi cho thấy, trước khi hiểu được các thuật toán phi tuyến (non-linear, không phẳng), chúng ta cần nắm vững các kỹ thuật cho các mô hình tuyến tính.

2. Hàm mất mát (Loss function) và Hàm chi phí (Cost function)

• Mục tiêu của tất cả các mô hình học có giám sát (supervised learning) trong machine learning là tìm ra một hàm số dự báo mà giá trị của chúng sai khác so với ground truth là nhỏ nhất. Ground truth ở đây chính là giá trị của biến mục tiêu $y$. Sai khác này được đo lường thông qua các hàm chi phí (cost function). Huấn luyện mô hình machine learning thực chất là qui về tìm cực trị của hàm chi phí. Tuỳ thuộc vào bài toán mà chúng ta có những dạng hàm chi phí khác nhau.

• rong bài toán dự báo chúng ta sẽ sử dụng hàm MSE (Mean Square Error) làm hàm mất mát. Hàm số này có giá trị bằng trung bình của tổng bình phương sai số giữa giá trị dự báo và ground truth. Gỉa sử chúng ta xét phương trình hồi qui đơn biến gồm $n$ quan sát có biến phụ thuộc là $\mathbf{y} = [y_1,y_2, \cdots , y_n]$ và biến đầu vào $\mathbf{x} = [x_1, x_2, \cdots, x_n]$. Vector $\mathbf{w} = (w_0, w_1)$ có giá trị $w_0, w_1$ lần lượt là hệ số góc và hệ số ước lượng. Phương trình hồi quy tuyến tính đơn biến có dạng:

\[\hat{y_i} = f(x_i) = w_0 + w_1*x_i\]

• Trong đó $(x_i, y_i)$ là điểm dữ liệu thứ $i$. Chúng ta mong muốn rằng sự sai khác giữa giá trị thực $y$ và giá trị dự đoán $\hat{y}$ (đọc là y hat trong tiếng Anh) là nhỏ nhất. Nói cách khác, chúng ta muốn các giá trị sau là nhỏ nhất:

\[\mathcal{L}_1 = (y_1 - \hat{y}_1)^2 \\ \mathcal{L}_2 = (y_2 - \hat{y}_2)^2 \\ ............... \\ \mathcal{L}_n = (y_n - \hat{y}_n)^2\]

• $\mathcal{L}_i$ được gọi là hàm mất mát (hàm mà được tính trên một điểm dữ liệu). Vậy làm thế nào để ta cho $n$ giá trị trên là nhỏ nhất, một cách đơn giản ta có thể cộng trung bình chúng lại, tức là ta cần tối thiểu hóa hàm sau:

\[\mathcal{L}(\mathbf{w}) = \frac{1}{2n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = \frac{1}{2n} \sum_{i=1}^{n} (y_i - w_0 - w_1 * x_i)^2\]

• Hàm trên được gọi là hàm mất mát (hàm mà tính trên toàn bộ điểm dữ liệu), hàm trên cũng được gọi là hàm MSE (Mean Squared Error), lưu ý là theo đúng như định nghĩa thì hàm MSE không có số $2$ ở dưới mẫu, tác dụng của số $2$ ở hàm trên là để dễ tính toán đạo hàm.
• Ký hiệu $$\mathcal{L}(\mathbf{w}) thể hiện rằng hàm mất mát là một hàm theo $\mathbf{w}$ trong điều kiện ta đã biết đầu vào là vector $\mathbf{x}$ và vector phụ biến phụ thuộc $\mathbf{y}$. Ta có thể tìm cực trị của phương trình trên dựa và đạo hàm theo $\mathbf{w}_0$ và $\mathbf{w}_1$ như sau:
• Đạo hàm theo $w_0$:

\[\frac{\delta \mathcal{L} (\mathbf{w})}{\delta w_0} = \frac{-1}{n} \sum_{i=1}^{n} (y_i - w_0 - w_1 * x_i) \\ \to \frac{\delta \mathcal{L} (\mathbf{w})}{\delta w_0} = \frac{-1}{n} \sum_{i=1}^{n} y_i + w_0 + w_1 \frac{1}{n} \sum_{i=1}^{n} x_i \\ \to \frac{\delta \mathcal{L} (\mathbf{w})}{\delta w_0} = -\bar{\mathbf{y}} + w_0 + w_1 \bar{\mathbf{x}} = 0 \tag{2}\]

• Đạo hàm theo $w_1$:

\[\frac{\delta \mathcal{L} (\mathbf{w})}{\delta w_1} = \frac{-1}{n} \sum_{i=1}^{n} x_i (y_i - w_0 - w_1 * x_i) \\ \to \frac{\delta \mathcal{L} (\mathbf{w})}{\delta w_1} = \frac{-1}{n} \sum_{i=1}^{n} x_i y_i + w_0 \frac{1}{n} \sum_{i=1}^{n} x_i + w_1 \frac{1}{n} \sum_{i=1}^{n} x_i^2 \\ \to \frac{\delta \mathcal{L} (\mathbf{w})}{\delta w_1} = -\overline{\mathbf{xy}} + w_0 \bar{\mathbf{x}} + w_1 \bar{\mathbf{x}^2} = 0 \tag{3}\]

• Từ phương trình ($2$) ta suy ra được: $w_0 = \bar{\mathbf{y}} - w_1\bar{\mathbf{x}}$. Thế vào phương trình $(3)$ ta tính được:

\[-\overline{\mathbf{xy}} + w_0 \bar{\mathbf{x}} + w_1 \bar{\mathbf{x}^2} = -\overline{\mathbf{xy}} + (\bar{\mathbf{y}} - w_1 \bar{\mathbf{x}}) \bar{\mathbf{x}} + w_1 \bar{\mathbf{x}^2} \\ \to -\overline{\mathbf{xy}} + w_0 \bar{\mathbf{x}} + w_1 \bar{\mathbf{x}^2} = -\overline{\mathbf{xy}} + \bar{\mathbf{y}} \bar{\mathbf{x}} - w_1 \bar{\mathbf{x}}^2 + w_1 \bar{\mathbf{x}^2} = 0\]

• Từ đó suy ra:

\[w_1 = \frac{\bar{\mathbf{x}} \bar{\mathbf{y}} - \overline{\mathbf{xy}}}{\bar{\mathbf{x}}^2 - \bar{\mathbf{x}^2}}\]

• Sau khi tínhđược $w_1$ thế vào ta tính được:

\[w_0 = \bar{\mathbf{y}} - w_1 \bar{\mathbf{x}}\]

• Đạo hàm bậc nhất bằng $0$ mới chỉ là điều kiện cần để $\mathbf{w}$ là cực trị của hàm mất mát. Để khẳng định cực trị đó là cực tiểu thì chúng ta cần chứng minh thêm đạo hàm bậc hai lớn hơn hoặc bằng 0 hay hàm số đó là hàm lồi. Điều này khá dễ dàng và mình xin dành cho bạn đọc. Bài tập bên dưới dây sẽ giúp bạn hiểu dễ hơn cách tìm nghiệm của phương trình hồi qui tuyến tính đơn biến.

• Giả sử chúng ta có 15 căn hộ với diện tích (đơn vị m2):

\[\mathbf{x} = [73.5,75.,76.5,79.,81.5,82.5,84.,85.,86.5,87.5,89.,90.,91.5]\]

• Mức giá của căn hộ lần lượt là (đơn vị tỷ VND đồng):

\[\mathbf{y} = [1.49,1.50,1.51,1.54,1.58,1.59,1.60,1.62,1.63,1.64,1.66,1.67,1.68]\]

• Xây dựng phương trình hồi quy tuyến tính đơn biến giữa diện tích và giá nhà:

import matplotlib.pyplot as plt
import numpy as np

%matplotlib inline
# area
x = np.array([[73.5,75.,76.5,79.,81.5,82.5,84.,85.,86.5,87.5,89.,90.,91.5]]).T
# price
y = np.array([[1.49,1.50,1.51,1.54,1.58,1.59,1.60,1.62,1.63,1.64,1.66,1.67,1.68]]).T

# Visualize data
def _plot(x, y, title="", xlabel="", ylabel=""):
  plt.figure(figsize=(14, 8))
  plt.plot(x, y, 'r-o', label="price")
  x_min = np.min(x)
  x_max = np.max(x)
  y_min = np.min(y)
  y_max = np.max(y)
  # mean price
  ybar = np.mean(y)
  plt.axhline(ybar, linestyle='--', linewidth=4, label="mean")
  plt.axis([x_min*0.95, x_max*1.05, y_min*0.95, y_max*1.05])
  plt.xlabel(xlabel, fontsize=16)
  plt.ylabel(ylabel, fontsize=16)
  plt.text(x_min, ybar*1.01, "mean", fontsize=16)
  plt.legend(fontsize=15)
  plt.title(title, fontsize=20)
  plt.show()

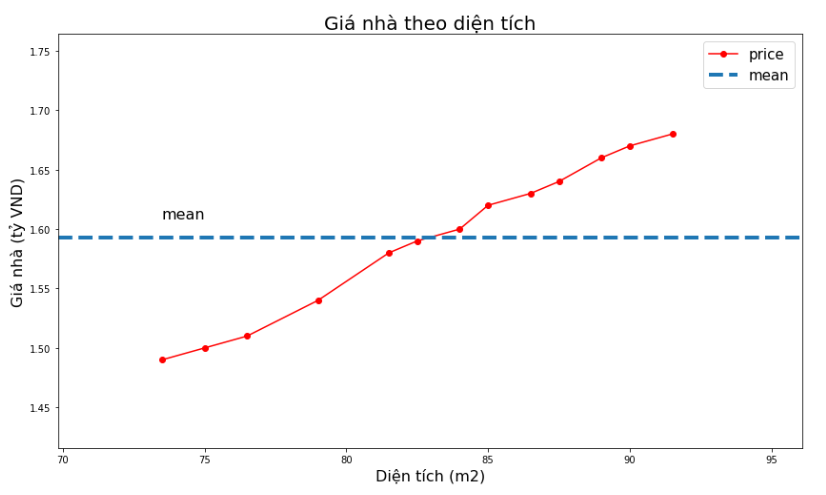
_plot(x, y, 
      title='Giá nhà theo diện tích',  
      xlabel='Diện tích (m2)', 
      ylabel='Giá nhà (tỷ VND)')

• Tính $w_0, w_1$:

# tính trung bình
xbar = np.mean(x)
ybar = np.mean(y)
x2bar = np.mean(x**2)
xybar = np.mean(x*y)

# tính w0, w1
w1 = (xbar*ybar-xybar)/(xbar**2-(x2bar))
w0 = ybar-w1*xbar

print('w1: ', w1)
print('w0: ', w0)
w1:  0.011184099238793658
w0:  0.6626458979418968

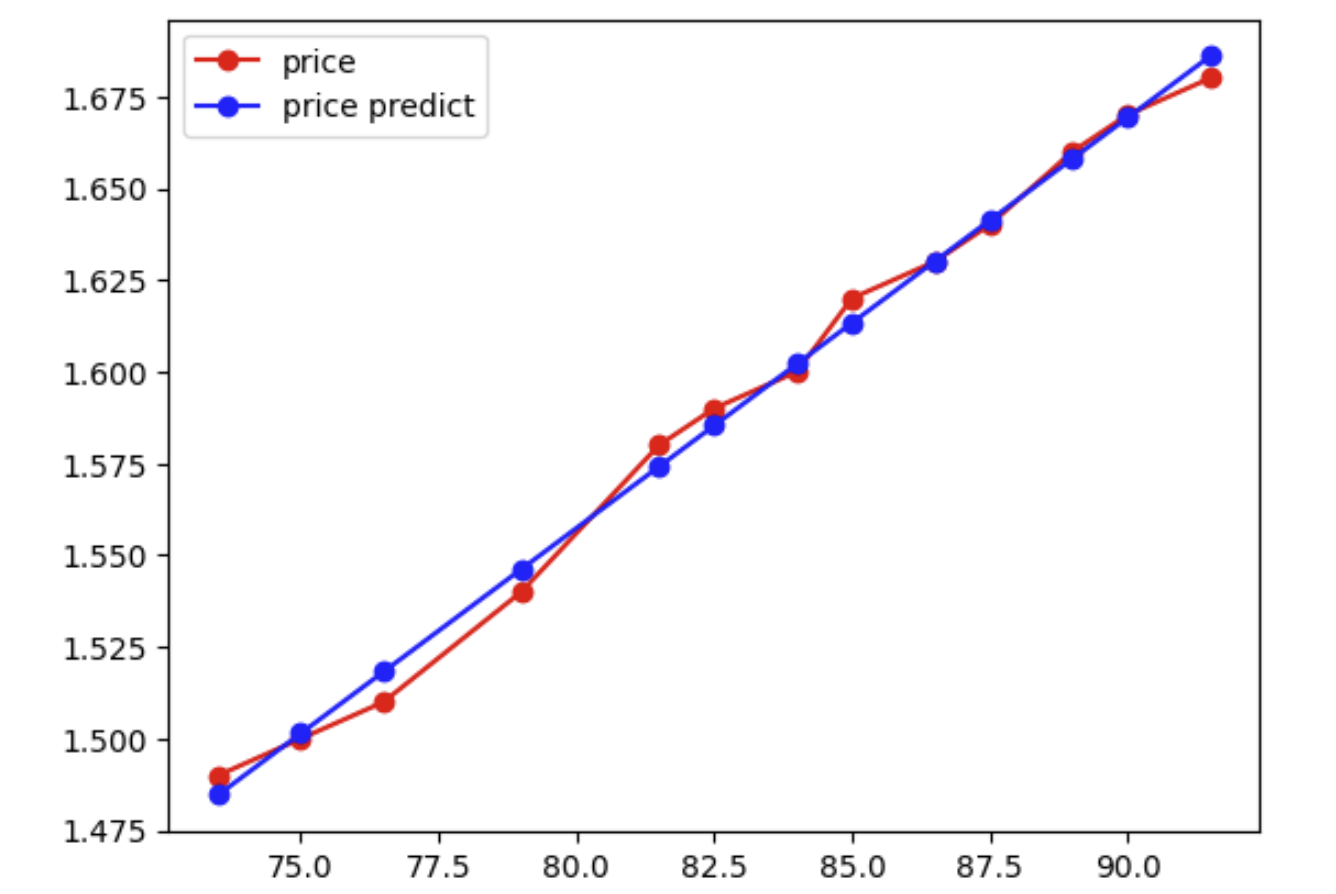
• Thử vẽ hai đồ thị, một đồ thị ban đầu và một đồ thị ta dự đoán:

y_pred = w0 + w1*x
plt.plot(x, y, 'r-o', label="price")
plt.plot(x, y_pred, 'b-o', label="price predict")
plt.legend()

• Như vậy ta có thể tìm được lời giải của phương trình hồi qui tuyến tính đơn biến thông qua đạo hàm bậc nhất. Tuy nhiên bài toán với phương trình hồi qui tuyến đa biến thì lời giải sẽ phức tạp hơn một chút vì chúng ta sẽ cần tới kiến thức về giải tích ma trận.

3. Hồi qui tuyến tính đa biến

• Hồi qui tuyến tính đa biến là hồi qui tuyến tính với nhiều hơn một biến đầu vào. Hồi qui tuyến tính đa biến phổ biến hơn so với đơn biến vì trên thực tế rất hiếm các tác vụ dự báo chỉ gồm một biến đầu vào. Phương trình hồi qui của nó có dạng:

\[\hat{y}_i = f(x_1, x_2, \dots, x_p) = w_0 + w_1 x_{i1} + \dots + w_p x_{ip} = \mathbf{w}^\top \mathbf{x}_i\]

• Ở đây ta xem $\mathbf{x}_i$ là một vector đại diện cho quan sát thứ $i$. Ma trận $\mathbf{X}$ có kích thước $n \times p$ có mỗi dòng là một quan sát và mỗi cột là một biến. Ma trận mở rộng của $\mathbf{X}$ được ký hiệu là $\bar{\mathbf{X}}$ chính là ma trận có thêm vector cột $1$ được thêm vào đầu tiên.

\[\hat{\mathbf{y}} = f(\mathbf{X}) = \begin{bmatrix} 1 & x_{11} & \cdots & x_{1p} \\ 1 & x_{21} & \cdots & x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & \cdots & x_{np} \end{bmatrix} \begin{bmatrix} w_0 \\ w_1 \\ \vdots \\ w_p \end{bmatrix} = \bar{\mathbf{X}} \mathbf{w}\]

• Hàm chi phí MSE là trung bình tổng bình phương của các sai số nên nó có dạng:

\[\mathcal{L} (\mathbf{w}) = \frac{1}{2} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = \frac{1}{2} \sum_{i=1}^{n} (y_i - \mathbf{w}^\top \mathbf{x}_i)^2 = \frac{1}{2} \|\bar{\mathbf{X}} \mathbf{w} - \mathbf{y} \|_2^2\]

• Cách phổ biến nhất để tìm nghiệm cho một bài toán tối ưu (chúng ta đã biết từ khi học cấp 3) là giải phương trình đạo hàm (gradient) bằng 0! Tất nhiên đó là khi việc tính đạo hàm và việc giải phương trình đạo hàm bằng 0 không quá phức tạp. Thật may mắn, với các mô hình tuyến tính, hai việc này là khả thi.

• Đạo hàm theo $\mathbf{w}$ của hàm chi phí là:

\[\frac{\partial \mathcal{L} (\mathbf{w})}{\partial \mathbf{w}} = \bar{\mathbf{X}}^\top (\bar{\mathbf{X}} \mathbf{w} - \mathbf{y})\]

• Phương trình đạo hàm bằng 0 tương đương với:

\[\mathbf{w} = (\bar{\mathbf{X}}^\top \bar{\mathbf{X}})^{-1} \bar{\mathbf{X}}^\top \mathbf{y} = (\mathbf{A}^{-1} \mathbf{b}) \tag{4}\]

• Ở trên để ta đã rút gọn $\mathbf{A} = \bar{\mathbf{X}}^\top \bar{\mathbf{X}}$ và $\bar{\mathbf{X}}^\top \mathbf{y} = \mathbf{b}$.

• Vậy nếu ma trận $\mathbf{A}$ không khả nghịch (có định thức bằng 0) thì sao? Nếu các bạn vẫn nhớ các kiến thức về hệ phương trình tuyến tính, trong trường hợp này thì hoặc phương trinh $(4)$ vô nghiệm, hoặc là nó có vô số nghiệm. Khi đó, chúng ta sử dụng khái niệm giả nghịch đảo $\mathbf{A}^{\dagger}$ (đọc là A dagger trong tiếng Anh). (Giả nghịch đảo (pseudo inverse) là trường hợp tổng quát của nghịch đảo khi ma trận không khả nghịch hoặc thậm chí không vuông.

• Với khái niệm giả nghịch đảo, điểm tối ưu của bài toán Linear Regression có dạng:

\[\mathbf{w} = \mathbf{A}^{\dagger} \mathbf{b} = \left( \bar{\mathbf{X}}^{T} \bar{\mathbf{X}} \right)^{\dagger} \bar{\mathbf{X}}^{T} \mathbf{y} \quad (5)\]

4. Ví dụ trên Python

• Trong phần này, tôi sẽ chọn một ví dụ đơn giản về việc giải bài toán Linear Regression trong Python. Tôi cũng sẽ so sánh nghiệm của bài toán khi giải theo phương trình $(5)$ và nghiệm tìm được khi dùng thư viện scikit-learn của Python. (Đây là thư viện Machine Learning được sử dụng rộng rãi trong Python). Trong ví dụ này, dữ liệu đầu vào chỉ có 1 giá trị (1 chiều) để thuận tiện cho việc minh hoạ trong mặt phẳng.

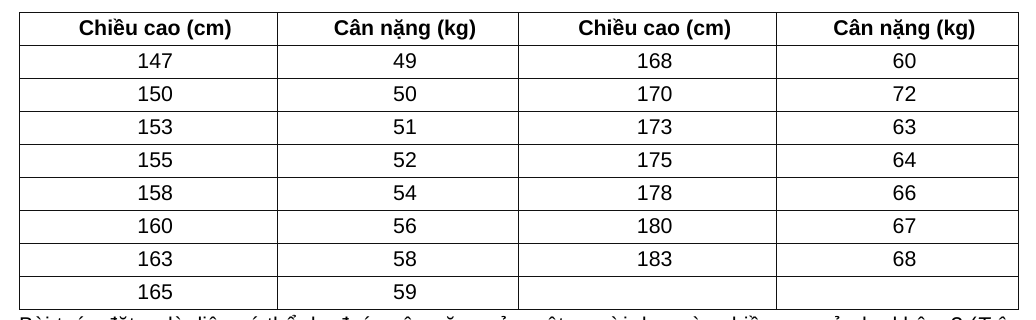
• Chúng ta có 1 bảng dữ liệu về chiều cao và cân nặng của 15 người như dưới đây:

• Bài toán đặt ra là: liệu có thể dự đoán cân nặng của một người dựa vào chiều cao của họ không? (Trên thực tế, tất nhiên là không, vì cân nặng còn phụ thuộc vào nhiều yếu tố khác nữa, thể tích chẳng hạn). Vì blog này nói về các thuật toán Machine Learning đơn giản nên tôi sẽ giả sử rằng chúng ta có thể dự đoán được.
• Chúng ta có thể thấy là cân nặng sẽ tỉ lệ thuận với chiều cao (càng cao càng nặng), nên có thể sử dụng Linear Regression model cho việc dự đoán này. Để kiểm tra độ chính xác của model tìm được, chúng ta sẽ giữ lại cột 155 và 160 cm để kiểm thử, các cột còn lại được sử dụng để huấn luyện (train) model.
• Trước tiên, chúng ta cần có hai thư viện numpy cho đại số tuyến tính và matplotlib cho việc vẽ hình.

from __future__ import division, print_function, unicode_literals
import numpy as np 
import matplotlib.pyplot as plt

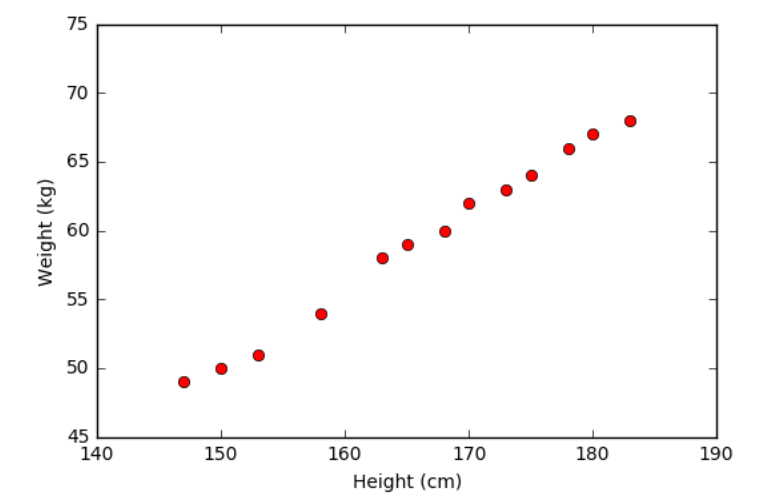
• Tiếp theo, chúng ta khai báo và biểu diễn dữ liệu trên một đồ thị.

# height (cm)
X = np.array([[147, 150, 153, 158, 163, 165, 168, 170, 173, 175, 178, 180, 183]]).T
# weight (kg)
y = np.array([[ 49, 50, 51,  54, 58, 59, 60, 62, 63, 64, 66, 67, 68]]).T
# Visualize data 
plt.plot(X, y, 'ro')
plt.axis([140, 190, 45, 75])
plt.xlabel('Height (cm)')
plt.ylabel('Weight (kg)')
plt.show()

• Từ đồ thị này ta thấy rằng dữ liệu được sắp xếp gần như theo 1 đường thẳng, vậy mô hình Linear Regression nhiều khả năng sẽ cho kết quả tốt:

\[\text{cân nặng} = w_1 * \text{chiều cao} + w_0\]

• Tiếp theo, chúng ta sẽ tính toán các hệ số $w_1$ và $w_0$ dựa vào công thức $(5)$. Chú ý: giả nghịch đảo của một ma trận A trong Python sẽ được tính bằng numpy.linalg.pinv(A), pinv là từ viết tắt của pseudo inverse.

# Building Xbar 
one = np.ones((X.shape[0], 1))
Xbar = np.concatenate((one, X), axis = 1)

# Calculating weights of the fitting line 
A = np.dot(Xbar.T, Xbar)
b = np.dot(Xbar.T, y)
w = np.dot(np.linalg.pinv(A), b)
print('w = ', w)
# Preparing the fitting line 
w_0 = w[0][0]
w_1 = w[1][0]
x0 = np.linspace(145, 185, 2)
y0 = w_0 + w_1*x0

# Drawing the fitting line 
plt.plot(X.T, y.T, 'ro')     # data 
plt.plot(x0, y0)               # the fitting line
plt.axis([140, 190, 45, 75])
plt.xlabel('Height (cm)')
plt.ylabel('Weight (kg)')
plt.show()

w = [[-33.73541021]

[ 0.55920496]]

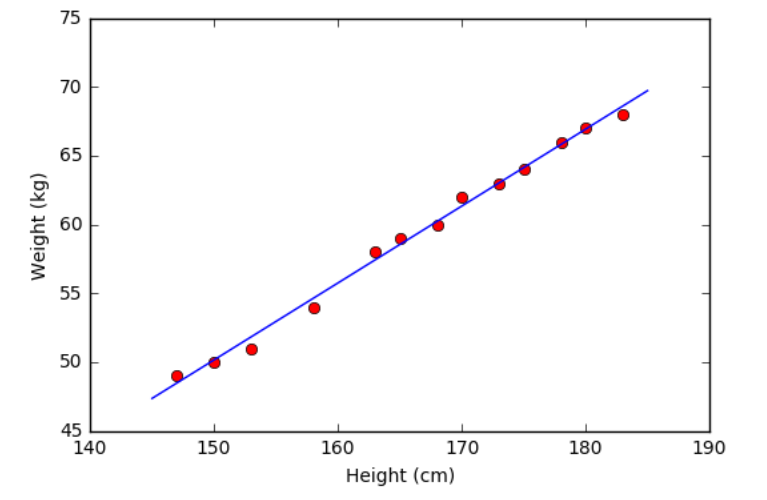
• Từ đồ thị bên trên ta thấy rằng các điểm dữ liệu màu đỏ nằm khá gần đường thẳng dự đoán màu xanh. Vậy mô hình Linear Regression hoạt động tốt với tập dữ liệu training. Bây giờ, chúng ta sử dụng mô hình này để dự đoán cân nặng của hai người có chiều cao 155 và 160 cm mà chúng ta đã không dùng khi tính toán nghiệm.

y1 = w_1*155 + w_0
y2 = w_1*160 + w_0

print( u'Predict weight of person with height 155 cm: %.2f (kg), real number: 52 (kg)'  %(y1) )
print( u'Predict weight of person with height 160 cm: %.2f (kg), real number: 56 (kg)'  %(y2) )

Predict weight of person with height 155 cm: 52.94 (kg), real number: 52 (kg)

Predict weight of person with height 160 cm: 55.74 (kg), real number: 56 (kg)

• Chúng ta thấy rằng kết quả dự đoán khá gần với số liệu thực tế. Tiếp theo, chúng ta sẽ sử dụng thư viện scikit-learn của Python để tìm nghiệm.

from sklearn import datasets, linear_model

# fit the model by Linear Regression
regr = linear_model.LinearRegression(fit_intercept=False) # fit_intercept = False for calculating the bias
regr.fit(Xbar, y)

# Compare two results
print( 'Solution found by scikit-learn  : ', regr.coef_ )
print( 'Solution found by (5): ', w.T)

Solution found by scikit-learn : [[ -33.73541021 0.55920496]]

Solution found by (5): [[ -33.73541021 0.55920496 ]]-

• Chúng ta thấy rằng hai kết quả thu được như nhau! (Nghĩa là tôi đã không mắc lỗi nào trong cách tìm nghiệm ở phần trên)

5. Thảo Luận

Các bài toán có thể giải bằng Linear Regression

• Hàm số $y \approx f(\mathbf{x}) = \mathbf{w}^T \mathbf{x}$ là một hàm tuyến tính theo cả $\mathbf{w}$ và $\mathbf{x}$. Trên thực tế, Linear Regression có thể áp dụng cho các mô hình chỉ cần tuyến tính theo $\mathbf{w}$. Ví dụ:

\[y \approx w_1 x_1 + w_2 x_2 + w_3 x_1^2 + w_4 \sin(x_2) + w_5 x_1 x_2 + w_0\]

• Là một hàm tuyến tính theo $\mathbf{w}$ và vì vậy cũng có thể được giải bằng Linear Regression. Với mỗi dữ liệu đầu vào $\mathbf{x} = [x_1;x_2]$, chúng ta tính toán dữ liệu mới $\hat{\mathbf{x}} = [x_1,x_2,x_1^2,\sin(x_2),x_1x_2]$ rồi áp dụng Linear Regression với dữ liệu mới này.

Hạn chế của Linear Regression

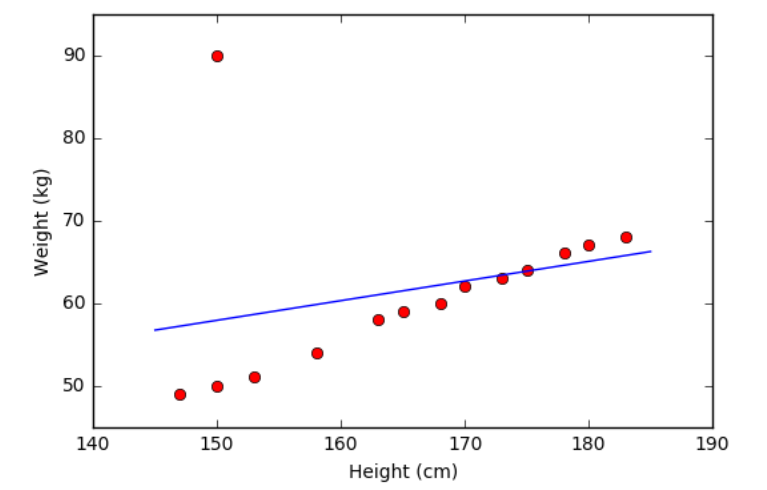
• Hạn chế đầu tiên của Linear Regression là nó rất nhạy cảm với nhiễu (sensitive to noise). Trong ví dụ về mối quan hệ giữa chiều cao và cân nặng bên trên, nếu có chỉ một cặp dữ liệu nhiễu (150 cm, 90kg) thì kết quả sẽ sai khác đi rất nhiều. Xem hình dưới đây:

• Vì vậy, trước khi thực hiện Linear Regression, các nhiễu (outlier) cần phải được loại bỏ. Bước này được gọi là tiền xử lý (pre-processing).

• Hạn chế thứ hai của Linear Regression là nó không biễu diễn được các mô hình phức tạp. Mặc dù trong phần trên, chúng ta thấy rằng phương pháp này có thể được áp dụng nếu quan hệ giữa outcome và input không nhất thiết phải là tuyến tính, nhưng mối quan hệ này vẫn đơn giản nhiều so với các mô hình thực tế. Hơn nữa, chúng ta sẽ tự hỏi: làm thế nào để xác định được các hàm $x_1^2, \sin(x_2), x_1x_2$ như ở trên?!

Các phương pháp tối ưu

• Linear Regression là một mô hình đơn giản, lời giải cho phương trình đạo hàm bằng 0 cũng khá đơn giản. Trong hầu hết các trường hợp, chúng ta không thể giải được phương trình đạo hàm bằng 0.

• Nhưng có một điều chúng ta nên nhớ, còn tính được đạo hàm là còn có hy vọng.

6. Đánh gía mô hình hổi qui tuyến tính đa biến

• Ngoài MSE là hàm chi phí dùng để làm mục tiêu tối ưu loss function thì chúng ta có thể dựa trên nhiều chỉ số khác để đánh giá một mô hình hồi qui tuyến tính đa biến. Cụ thể như sau:

Chỉ số R-squared

• R-squared cho ta biết mức độ các biến đầu vào sẽ giải thích được bao nhiêu phần trăm các biến mục tiêu. R-squared càng lớn thì mô hình càng tốt, khi R-squared bằng $95\%$ điều đó có nghĩa rằng các biến đầu vào đã giải thích được $95\%$ sự biến động của biến mục tiêu.
• R-squared được xây dựng dựa trên ba chỉ số:

\[TSS = \sum_{i=1}^{n} (y_i - \bar{y})^2 \\ RSS = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \\ ESS = \sum_{i=1}^{n} (\hat{y}_i - \bar{y})^2\]

• Trong đó $TSS$ là tổng bình phương sai số toàn bộ mô hình (Total Sum Squared), $RSS$ là tổng bình phương sai số ngẫu nhiên (Residual Sum Squared), $ESS$ là tổng bình phương sai số được giải thích bởi mô hình (Explained Sum Squared).
• Ta sẽ chứng minh được $TSS = RSS + ESS$. Thật vậy:

\[TSS = \sum_{i=1}^{n} (y_i - \bar{y})^2 = \sum_{i=1}^{n} [(y_i - \hat{y}_i) + (\hat{y}_i - \bar{y})]^2 \\ \to TSS = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 + \sum_{i=1}^{n} (\hat{y}_i - \bar{y})^2 + 2 \sum_{i=1}^{N} (y_i - \hat{y}_i)(\hat{y}_i - \bar{y}) \\ \to TSS = ESS + RSS + 2 \sum_{i=1}^{N} (y_i \hat{y}_i - y_i \bar{y} - \hat{y}_i \hat{y}_i + \hat{y}_i \bar{y}) \\ \to TSS = ESS + RSS + 2 \sum_{i=1}^{N} (y_i \hat{y}_i - y_i \bar{y} - \hat{y}_i \hat{y}_i + \hat{y}_i \bar{y}) \\ \to TSS = ESS + RSS + 2 \underbrace{\sum_{i=1}^{N} \hat{y}_i (y_i - \bar{y}_i)}_{A} + 2 \underbrace{\bar{y} \sum_{i=1}^{N} (\hat{y}_i - y_i)}_{B}\]

• Ta sẽ chứng minh cả hai hạng tử $A$ và $B$ đều bằng $0$. Thật vậy, từ phương trình đạo hàm bậc nhất của loss function theo $w_0$ và $w_1$ ta có:

\[\sum_{i=1}^{N} x_i (y_i - \hat{y}_i) = 0 \tag{5}\] \[\sum_{i=1}^{N} (y_i - \hat{y}_i) = 0 \tag{6}\]

• Do đó:

\[\bar{y} \sum_{i=1}^{N} (\hat{y}_i - y_i) = 0 \iff B = 0\]

• Nhân biểu thức $(5)$ với $w_1$ và biểu thức $(6)$ với $w_0$ và cộng vế với vế:

\[w_0 \sum_{i=1}^{N} (y_i - \hat{y}_i) + \sum_{i=1}^{N} w_1 x_i (y_i - \hat{y}_i) = 0 \\ \iff \sum_{i=1}^{N} (w_0 + w_1 x_i) (y_i - \hat{y}_i) = 0 \\ \iff \sum_{i=1}^{N} \hat{y}_i (y_i - \hat{y}_i) = 0 \\ \iff B = 0\]

• Dòng $2$ suy ra $3$ là vì $\hat{y}_i = w_0 + w_1 x_i$. Như vậy $A = B = 0$ suy ra $TSS = ESS + RSS$. Khi đó:

\[R^2 = 1 - \frac{RSS}{TSS}\]

• Như vậy $R^2$ càng lớn thì giá trị tổng bình phương sai số càng nhỏ.

Chỉ số MAE và MAPE

• MAE là chỉ số đo lường trung bình trị tuyệt đối sai số giữa giá trị dự báo và giá trị thực tế.

\[\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} | y_i - \hat{y}_i |\]

• Chúng ta có thể thấy về bản chất thì MAE chính là norm chuẩn bậc 1. Khi MAE càng nhỏ thì khoảng cách giữa giá trị dự báo và giá trị thực tế càng nhỏ và mô hình càng tốt. Tuy nhiên giá trị MAE không bao hàm được sự khác biệt về mặt đơn vị. Ví dụ như khi chúng ta đo lường sai số về cân nặng của những con voi và cân nặng của những con chuột thì khả năng rất cao là voi có sai số lớn hơn so với chuột. Nhưng sai số này lớn là do chúng ta chưa xét đến kích cỡ của voi và chuột. Chính vì thế để loại bỏ sự khác biệt về mặt đơn vị thì chúng ta sử dụng chỉ số MAPE.
• MAPE là chỉ số đo lường tỷ lệ phần trăm sai số giữa giá trị dự báo và giá trị thực tế . Nó là viết tắt của cụm từ mean absolute percentage error có công thức như sau:

\[\text{MAPE} = \frac{1}{n} \sum_{i=1}^{n} | \frac{y_i - \hat{y}_i}{y_i} |\]

• Khi một mô hình có $\text{MAPE} = 5\%$ ta nói rằng mô hình có trung bình sai số là $5\%$ so với giá trị trung bình.

7. Ridge regression và Lasso regression

• Ridge regression và Lasso regression là hai mô hình hồi qui áp dụng kỹ thuật hiệu chuẩn (regularization) để tránh hiện tượng quá khớp (overfitting). Trước tiên ta tìm hiểu một chút về quá khớp:

• Quá khớp là hiện tượng mà mô hình chỉ khớp tốt trên tập dữ liệu huấn luyện nhưng không dự báo tốt trên dữ liệu kiểm tra. Đây là trường hợp thường gặp khi huấn luyện các mô hình machine learning. Hiện tượng này gây ảnh hưởng xấu và dẫn tới mô hình không thể áp dụng được vì các dự báo bị sai khi áp dụng vào thực tiễn. Có nhiều nguyên nhân dẫn tới quá khớp. Một trong những nguyên nhân phổ biến đó là tập dữ liệu huấn luyện và dữ liệu dự báo có phân phối khác xa nhau dẫn tới các qui luật học được ở dữ liệu huấn luyện không còn đúng trên dữ liệu dự báo. Hoặc cũng có thể xuất phát từ phía mô hình quá nhiều tham số nên khả năng biểu diễn dữ liệu của nó không mang tính đại diện.

• Regularization là kĩ thuật tránh overfiting bằng cách cộng thêm vào loss function thành phần hiệu chuẩn. Thông thường thành phần này ở dạng norm chuẩn bậc 1 hoặc 2 của các hệ số. Trong trường hợp bậc 2 ta gọi là Ridge regression:

\[\mathcal{L} (\mathbf{w}) = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 + \alpha\|\mathbf{w}\|_2^2\]

• Đối với trường hợp bậc 1 gọi là Lasso regression:

\[\mathcal{L} (\mathbf{w}) = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 + \alpha\|\mathbf{w}\|_1\]

• Đối với những hồi qui này thì chúng ta cần tinh chỉnh hệ số $\alpha$ để tìm ra một hệ số là tốt nhất với từng bộ dữ liệu.
• Trong trường hợp dữ liệu bị quá khớp nặng thì cần giảm quá khớp bằng cách gia tăng ảnh hưởng của thành phần điều chuẩn (regularization term) thông qua tăng hệ số $\alpha$. Nếu mô hình không bị quá khớp thì có thể lựa chọn $\alpha$ gần 0. Trường hợp $\alpha = 0$ thì phương trình hồi qui tương đương với hồi qui tuyến tính đa biến.
• Bên dưới ta sẽ cùng xây dựng phương trình hồi qui đối với Ridge regression.

# Khởi tạo mô hình Ridge với một giá trị alpha (điều chỉnh độ phạt L2)
alpha = 0.1 # Bạn có thể thay đổi giá trị này để kiểm soát mức độ regularization
model = linear_model.Ridge(alpha=alpha, fit_intercept=False)

# Huấn luyện mô hình
model.fit(Xbar, y)

# Lấy hệ số của mô hình
print("Hệ số (coef_):", model.coef_)

Hệ số (coef_): [-12.49877733 0.43214701]

• Nếu bạn muốn tìm alpha tối ưu, dùng RidgeCV:

model = linear_model.RidgeCV(alphas=[0.1, 1.0, 10.0], fit_intercept=False)
model.fit(Xbar, y)
print("Alpha tối ưu:", model.alpha_)
print("Hệ số (coef_):", model.coef_)

• Xây dựng phương trình đối với Lasso regression:

# Khởi tạo mô hình Lasso với một giá trị alpha (điều chỉnh độ phạt L1)
alpha = 0.1  # Bạn có thể thay đổi giá trị này để kiểm soát độ sparsity của trọng số
model = linear_model.Lasso(alpha=alpha, fit_intercept=False)

# Huấn luyện mô hình
model.fit(Xbar, y)

# Lấy hệ số của mô hình
print("Hệ số (coef_):", model.coef_)

Hệ số (coef_): [-11.26389706 0.4247553 ]

• Nếu bạn muốn tự động tìm alpha tối ưu, dùng LassoCV:

model = linear_model.LassoCV(cv=5, fit_intercept=False)
model.fit(Xbar, y)
print("Alpha tối ưu:", model.alpha_)
print("Hệ số (coef_):", model.coef_)

8. Tổng kết

• Như vậy ở chương này các bạn đã được học:
  1. Phương trình hồi qui tuyến tính đơn biến và hồi qui tuyến tính đa biến.
  2. Hàm mất mát MSE của hồi qui tuyến tính đơn biến.
  3. Các chỉ số đánh giá mô hình hồi qui tuyến tính như R-squared, MAP, MAPE
  4. Các phương pháp hồi qui tuyến tính với thành phần điều chuẩn như Ridge Regresssion và Lasso Regression.
  5. Các biểu diễn kết quả mô hình thông qua biểu đồ.
  6. Tuning hệ số của mô hình hồi qui.

9. Tài liệu tham khảo

• [1] Linear Regression
• [2] Ứng dụng của hồi quy tuyến tính