KAN: Kolmogorov–Arnold Networks

Posted Jan 5, 2025 Updated Jan 29, 2025

By Bui Quang Dat

18 min read

Mạng Kolmogorov-Arnold (KANs), được lấy cảm hứng từ định lý biểu diễn Kolmogorov-Arnold, là một lựa chọn đầy hứa hẹn thay thế cho mạng nơ-ron (MLP). Được phát triển tại MIT, KANs đang gây chú ý ở khắp mọi nơi, từ Twitter đến các diễn đàn. Các tác giả đã đưa ra những tuyên bố mạnh mẽ, và dường như mọi người đều đã hướng sự chú ý vào nó. Nhưng liệu chúng có thực sự đáp ứng được những tuyên bố như “thay thế được MLP” đó không? Chúng là gì và chúng hoạt động như thế nào? Trong bài viết này, tôi sẽ trả lời tất cả những câu hỏi trên và hy vọng sẽ làm sáng tỏ một số thuật ngữ và ký hiệu khó hiểu đi kèm với chúng.

1. Mạng Kolmogorov-Arnold (KANs)

Mạng Kolmogorov-Arnold (KANs) là một loại mạng nơ-ron (NN) rất mới, được đề xuất tại paper, tập trung vào định lý biểu diễn Kolmogorov-Arnold thay vì định lý xấp xỉ phổ quát thường thấy trong các NN. Nói một cách đơn giản, các NN sử dụng hàm kích hoạt cố định trên các nút của chúng. Nhưng KANs lại có các hàm kích hoạt có thể học được trên các cạnh giữa các nút. Phần này sẽ đi sâu hơn vào kiến trúc của KAN và những khác biệt chính giữa KAN và NN, nhưng trước tiên, chúng ta cần thảo luận hai khái niệm: định lý biểu diễn Kolmogorov-Arnold và B-splines.

Định lý biểu diễn Kolmogorov-Arnold.

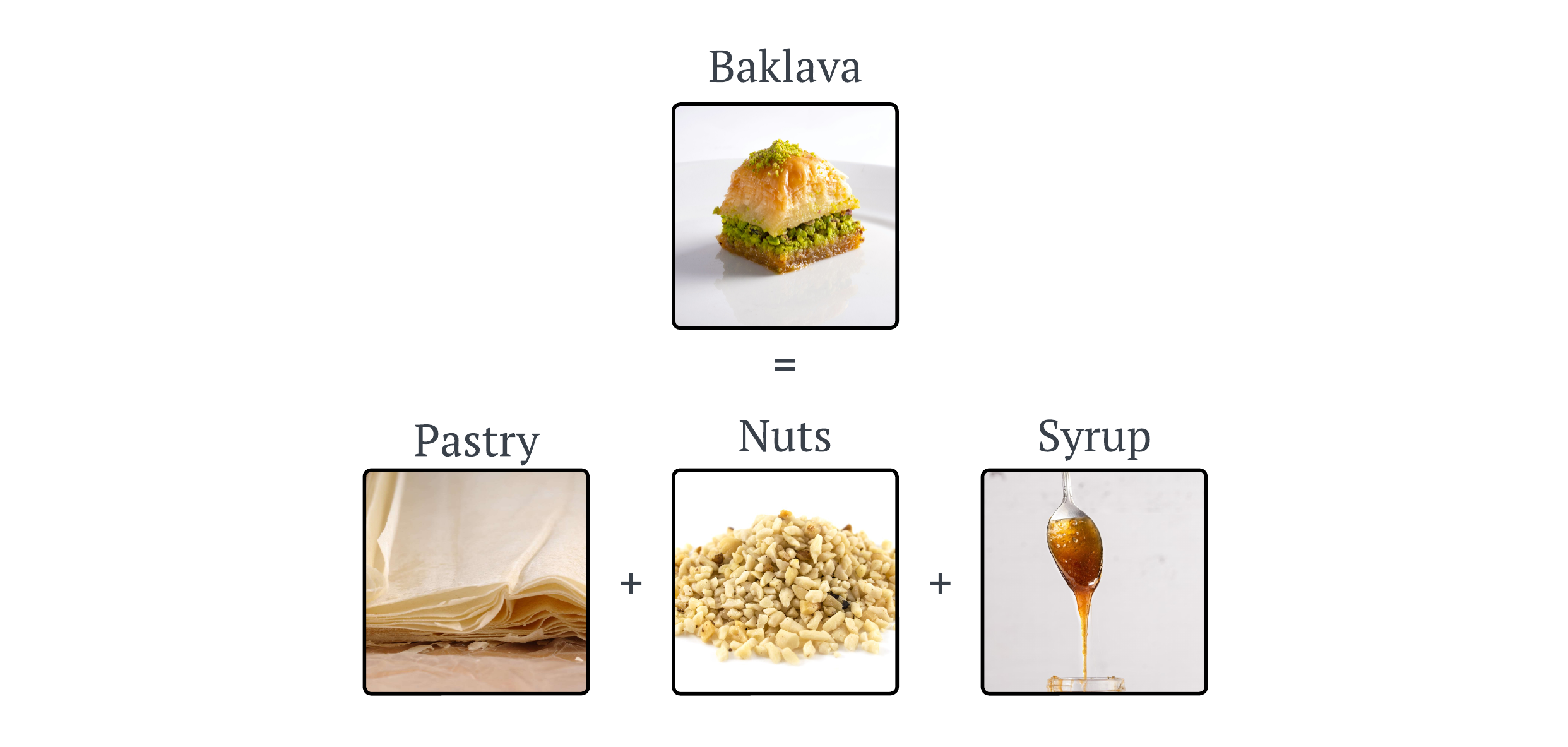
Như đã đề cập, KANs sử dụng định lý biểu diễn Kolmogorov-Arnold. Theo định lý này, bất kỳ hàm đa biến $f$ nào cũng có thể được biểu diễn dưới dạng tổng hữu hạn các hàm liên tục một biến. Nhưng hãy tạm gác toán học sang một bên. Nếu bạn không phải là một nhà toán học, điều này thực sự có ý nghĩa gì ?
Hãy tưởng tượng tôi yêu cầu bạn làm Baklava, một món tráng miệng với nhiều nguyên liệu và các bước chế biến. Thoạt nhìn, việc làm Baklava có vẻ phức tạp. Tuy nhiên, định lý biểu diễn Kolmogorov-Arnold gợi ý rằng bất kỳ “công thức” phức tạp nào cũng có thể được đơn giản hóa thành các “công thức” cơ bản với từng nguyên liệu một, sau đó được kết hợp lại theo những cách cụ thể. Dưới đây là minh họa trực quan về quá trình này:

Hình ảnh này minh họa cách quá trình phức tạp để làm món Baklava có thể được chia nhỏ thành các nhiệm vụ đơn giản hơn, chẳng hạn như “băm nhỏ các loại hạt” hoặc “xếp các lớp bánh”. Mỗi nhiệm vụ này xử lý một khía cạnh cụ thể của công thức, tương tự như xử lý một biến tại một thời điểm trong một hàm toán học. Quay trở lại với toán học, định lý này có thể được diễn đạt như sau:

\[f(x_1, \dots, x_n) = \sum_{q=1}^{2n+1} \Phi_q \left( \sum_{p=1}^n \phi_{q,p}(x_p) \right)\]

Trong đó $f(x_1, \dots, x_n)$ là hàm số nhiều biến (công thức phức tạp), $\phi_{q,p}(x_p)$ là các hàm số một biến (công thức có thể phức tạp nhưng đầu vào chỉ là một biến), và $\Phi_q$ là hàm số kết hợp các hàm số một biến lại với nhau. Bằng cách hiểu sự phân tích này, chúng ta thấy rằng các vấn đề phức tạp (hoặc công thức phức tạp) có thể được xử lý từng phần một, giúp cho toàn bộ quy trình trở nên dễ quản lý hơn.

B-splines

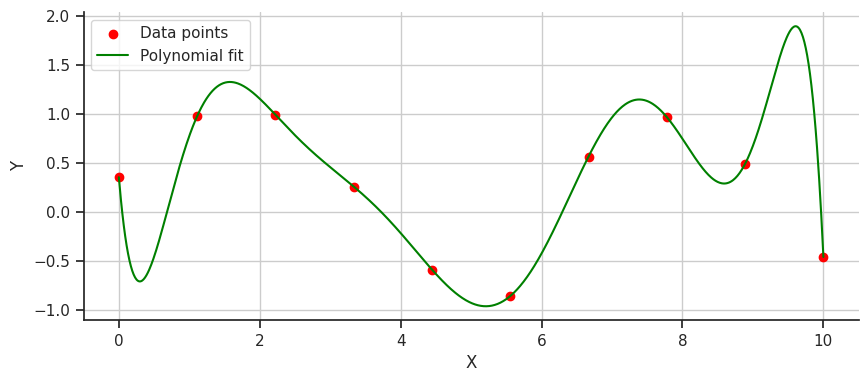
Một cách chính thức, B-splines là một phương pháp nội suy đường cong tiên tiến và là một loại spline- một thuật ngữ toán học chỉ một hàm đa thức từng đoạn linh hoạt, định nghĩa một đường cong mượt mà đi qua một loạt các điểm. Một cách không chính thức, hãy tưởng tượng bạn đã vẽ các điểm trên một biểu đồ để biểu thị mức chi tiêu của bạn đã dao động như thế nào trong 10 tháng qua, và bây giờ bạn muốn có một đường mượt mà nhất để thể hiện xu hướng trong những tháng đó. Để làm được điều này, chúng ta có thể sử dụng công thức nội suy Lagrange. Hãy xem điều đó sẽ trông như thế nào.

Chúng ta đã có một đường cong mượt mà thể hiện thói quen chi tiêu trong 10 tháng qua. Nhưng nếu nhìn kỹ hơn, đặc biệt là sau điểm dữ liệu đầu tiên, tại sao đường cong lại giảm mạnh như vậy thay vì chỉ cong lên hướng về điểm dữ liệu thứ hai? Vấn đề này với nội suy đa thức là do chúng thường có xu hướng dao động mạnh, một vấn đề được gọi là hiện tượng Runge.
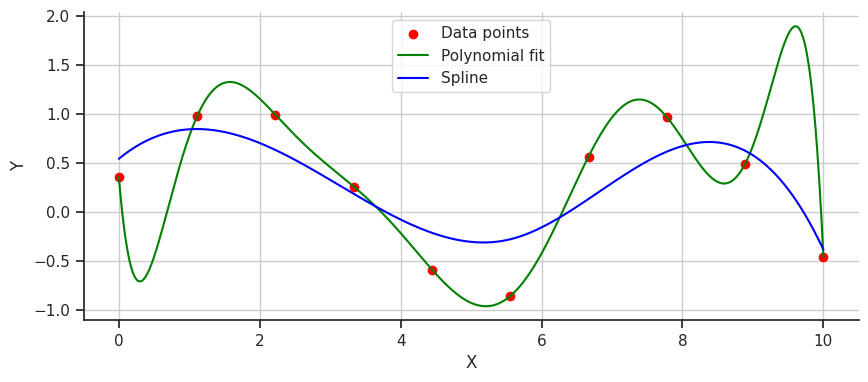
Làm thế nào để chúng ta vẽ đường cong này tốt hơn ? Hãy thử dùng spline! Một spline sẽ chia dữ liệu thành từng đoạn và gán các đa thức riêng lẻ cho mỗi đoạn. Hãy xem đường cong được nội suy bằng spline trông như thế nào.

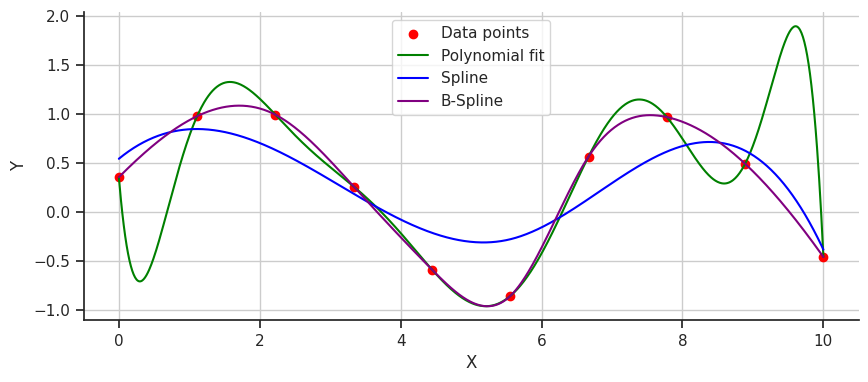
Kết quả nội suy này mượt mà hơn nhiều, nhưng có lẽ nó lại đơn giản và không khớp đủ với dữ liệu (underfit). Đây chính là lúc B-splines có thể can thiệp để cải thiện. B-splines, một loại spline sử dụng các điểm điều khiển để kéo đường cong và hướng dẫn các đa thức khớp tốt hơn, mang lại một giải pháp chính xác hơn. Hãy cùng xem cách B-splines nội suy dữ liệu trông như thế nào.

Hoàn hảo! B-spline không dao động mạnh mẽ cũng không bị underfit; thay vào đó, nó khớp hoàn hảo với dữ liệu. B-splines mang lại sự mượt mà vượt trội và độ chính xác cần thiết để mô hình hóa các hàm phức tạp. Chúng có thể dễ dàng thích nghi với các thay đổi trong mẫu dữ liệu mà không cần phải thay đổi toàn bộ mô hình, khiến chúng trở thành một công cụ linh hoạt và mạnh mẽ cho việc nội suy dữ liệu.
Về mặt toán học, chúng ta có thể định nghĩa một B-spline như sau:

\[C(t) = \sum_{i=0}^n P_i N_{i,k}(t)\]

Trong đó:
- $P_i$ là các điểm điều khiển (control points).
- $N_{i,k}(t)$ là các hàm cơ sở (basis functions).
- $t$ là vector nút (knot vector).

Kiến trúc của KAN

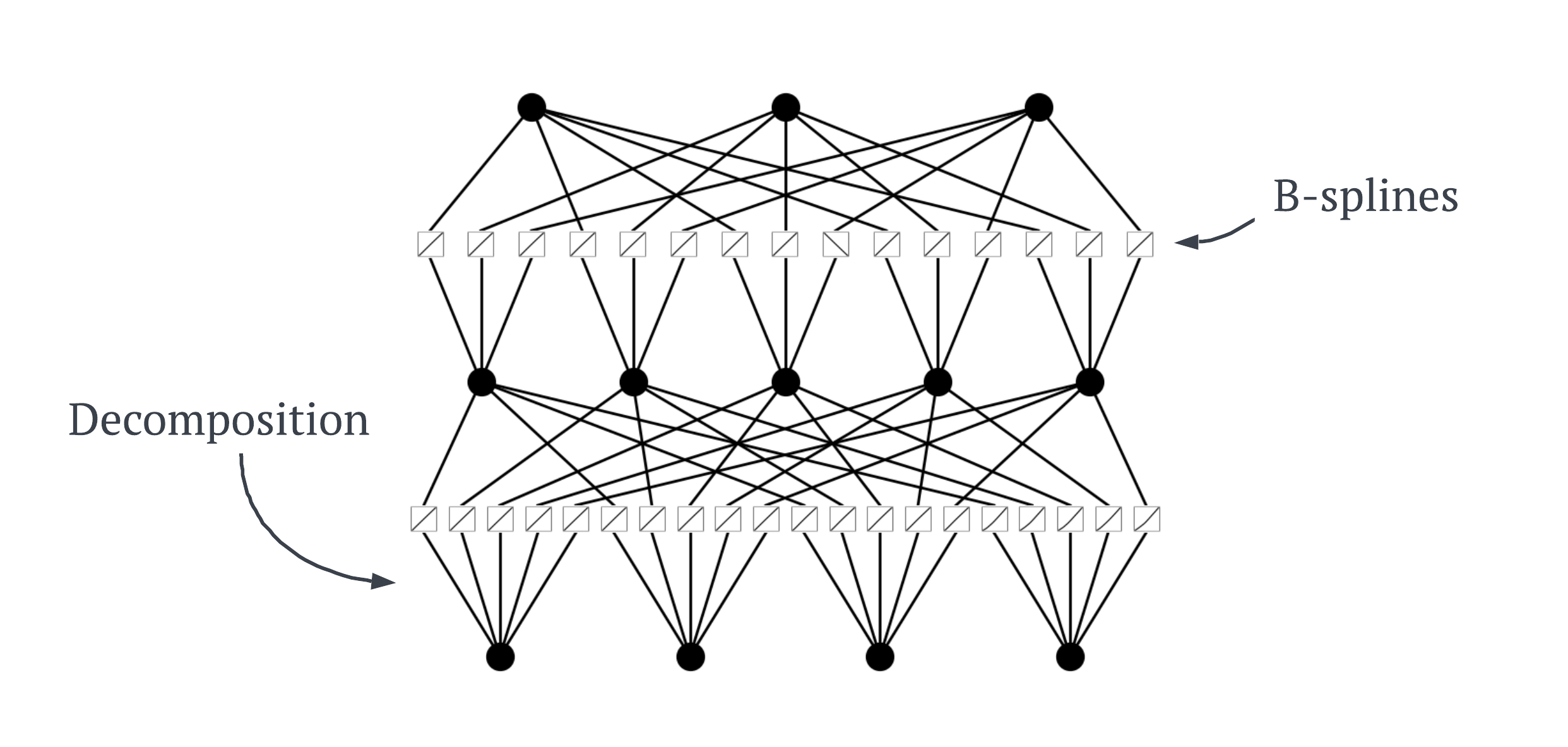
KANs đại diện cho một bước đột phá trong thiết kế mạng nơ-ron bằng cách tận dụng Định lý Biểu diễn Kolmogorov-Arnold (KAR) cùng với B-splines, tạo nên một mô hình linh hoạt và mạnh mẽ. Định lý KAR chỉ ra cách phân tách các hàm phức tạp thành các hàm đơn giản hơn. KANs áp dụng nguyên tắc này tại mỗi cạnh trong mạng, biến mỗi cạnh giữa các nơ-ron thành một hàm kích hoạt B-spline có thể học được. Điều này cho phép mỗi cạnh học chính xác phần dữ liệu đầu vào cụ thể của nó, giống như việc làm một phần cụ thể trong công thức món Baklava. Kiến trúc KAN có thể được minh họa như dưới đây.

Khi KANs được huấn luyện, sự thú vị thực sự bắt đầu. Mỗi B-spline điều chỉnh các điểm điều khiển $P_i$ của mình thông qua một quá trình gọi là lan truyền ngược (backpropagation). Đây là một phương pháp phổ biến trong việc huấn luyện mạng nơ-ron, nhưng trong trường hợp này, nó mang một ý nghĩa hoàn toàn mới. Quá trình thích nghi này cho phép KANs tinh chỉnh cách tiếp cận dữ liệu của mình sau mỗi lần huấn luyện, liên tục cải thiện độ chính xác và hiệu quả.
Giờ đây, khi bạn đã hiểu cách KANs được cấu trúc và thích nghi trong quá trình huấn luyện, hãy cùng đi sâu vào một ví dụ thực tế. Trong các phần tiếp theo, chúng ta sẽ khám phá cách thiết lập và huấn luyện một KAN, sử dụng dữ liệu thực để trực tiếp quan sát cách mạng này học hỏi và phát triển.

2. Huấn luyện mạng KAN

Để xây dựng và huấn luyện KAN, trước tiên chúng ta có thể sử dụng gói pykan do các tác giả của bài báo KAN gốc cung cấp. Chúng ta có thể cài đặt bằng cách sử dụng:

pip install pykan

Chúng ta sẽ làm bài toán phân loại với tập dữ liệu đơn giản đó chính là Iris. Đầu tiên, chúng ta sẽ import các thư viện cần thiết:

  
import torch
from kan import *
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import moviepy.video.io.ImageSequenceClip

if torch.cuda.is_available():
  device = torch.device("cuda")
else:
  device = torch.device("cpu")

print(device)

Tiếp theo, chúng ta sẽ tạo ra một hàm để load data cũng như chia data thành hai tập là tập train và test:

  
def load_iris_dataset():
    # Load iris dataset
    iris = load_iris()
    data = iris.data
    target = iris.target

    # Convert to PyTorch tensors
    data_tensor = torch.tensor(data, dtype=torch.float32)
    target_tensor = torch.tensor(target, dtype=torch.long)

    # Split dataset into train and test sets
    train_data, test_data, train_target, test_target = train_test_split(data_tensor, target_tensor, test_size=0.2, random_state=42)

    # Create data loaders (optional, if you want to batch and shuffle the data)
    train_loader = torch.utils.data.DataLoader(torch.utils.data.TensorDataset(train_data, train_target), batch_size=1, shuffle=True)
    test_loader = torch.utils.data.DataLoader(torch.utils.data.TensorDataset(test_data, test_target), batch_size=1, shuffle=False)

    train_inputs = torch.empty(0, 4, device=device)
    train_labels = torch.empty(0, dtype=torch.long, device=device)
    test_inputs = torch.empty(0, 4, device=device)
    test_labels = torch.empty(0, dtype=torch.long, device=device)

    # Concatenate all data into a single tensor on the specified device
    for data, labels in train_loader:
        train_inputs = torch.cat((train_inputs, data.to(device)), dim=0)
        train_labels = torch.cat((train_labels, labels.to(device)), dim=0)

    for data, labels in test_loader:
        test_inputs = torch.cat((test_inputs, data.to(device)), dim=0)
        test_labels = torch.cat((test_labels, labels.to(device)), dim=0)

    dataset = {}
    dataset['train_input'] = train_inputs
    dataset['test_input'] = test_inputs
    dataset['train_label'] = train_labels
    dataset['test_label'] = test_labels

    return dataset

iris_dataset = load_iris_dataset()

Giờ chúng ta sẽ khởi tạo mạng KAN như sau:

  
image_folder = 'video_img'

# width = [4,5,3]: Mô hình có 3 lớp, lớp đầu vào có 4 nơ-ron, lớp ẩn có 5 nơ-ron, lớp đầu ra có 3 nơ-ron
# grid = 5: số điểm điều khiển P_i
# k = 3: Bậc của B-spline
model = KAN(width=[4, 5, 3], grid=5, k=3, seed=0, device=device)

model(iris_dataset['train_input'])

# Trực quan hóa model
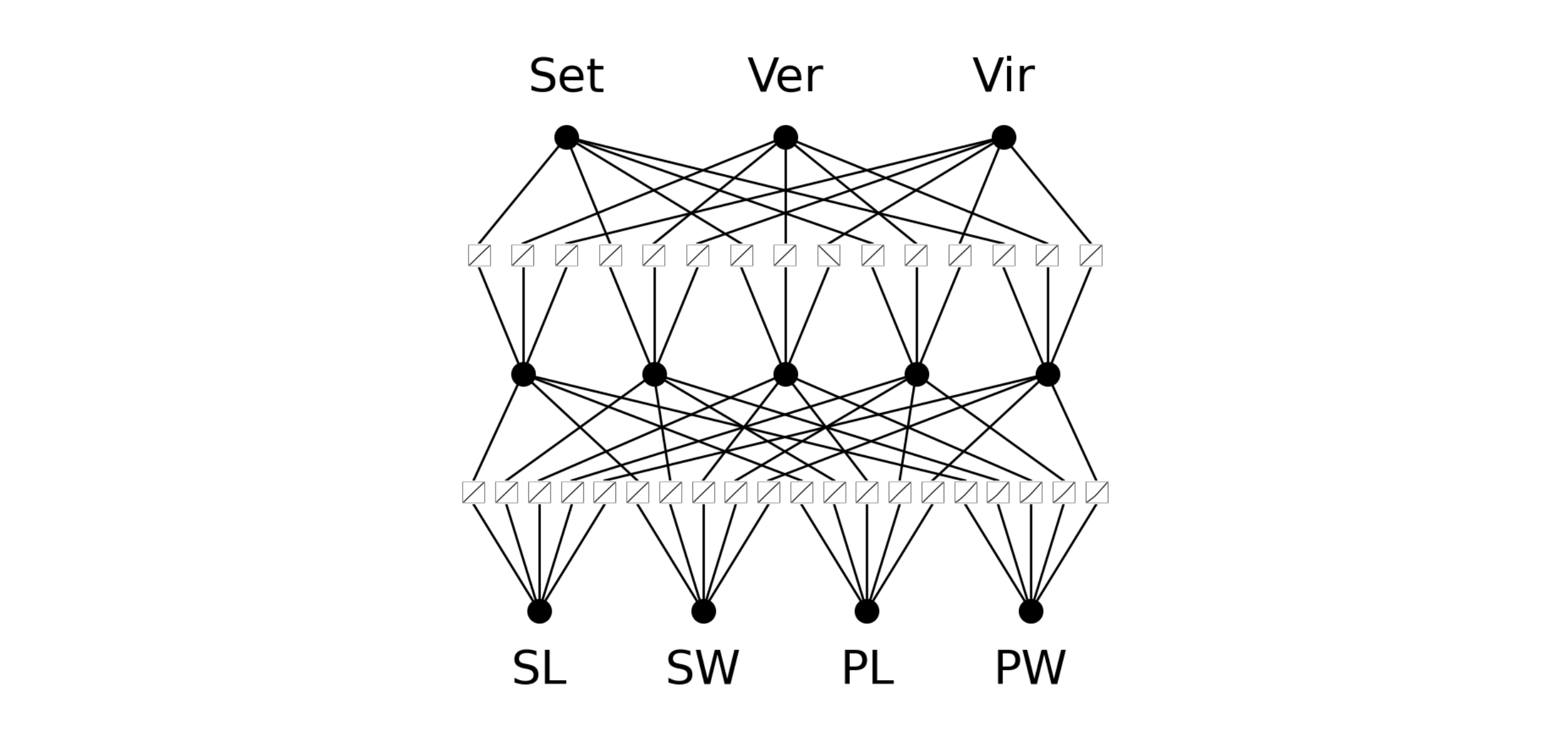
model.plot(beta=100, scale=1, in_vars=['SL', 'SW', 'PL', 'PW'], out_vars=['Set', 'Ver', 'Vir'])

Dưới đây là hình ảnh được trực quan hóa của mô hình:

Tiếp theo chúng ta sẽ huấn luyện mô hình:

  
def train_acc():
    return torch.mean((torch.argmax(model(iris_dataset['train_input']), dim=1) == iris_dataset['train_label']).float())

def test_acc():
    return torch.mean((torch.argmax(model(iris_dataset['test_input']), dim=1) == iris_dataset['test_label']).float())

results = model.fit(iris_dataset, opt="Adam", metrics=(train_acc, test_acc),
                      loss_fn=torch.nn.CrossEntropyLoss(), steps=100, lamb=0.01, lamb_entropy=10., save_fig=True, img_folder=image_folder)

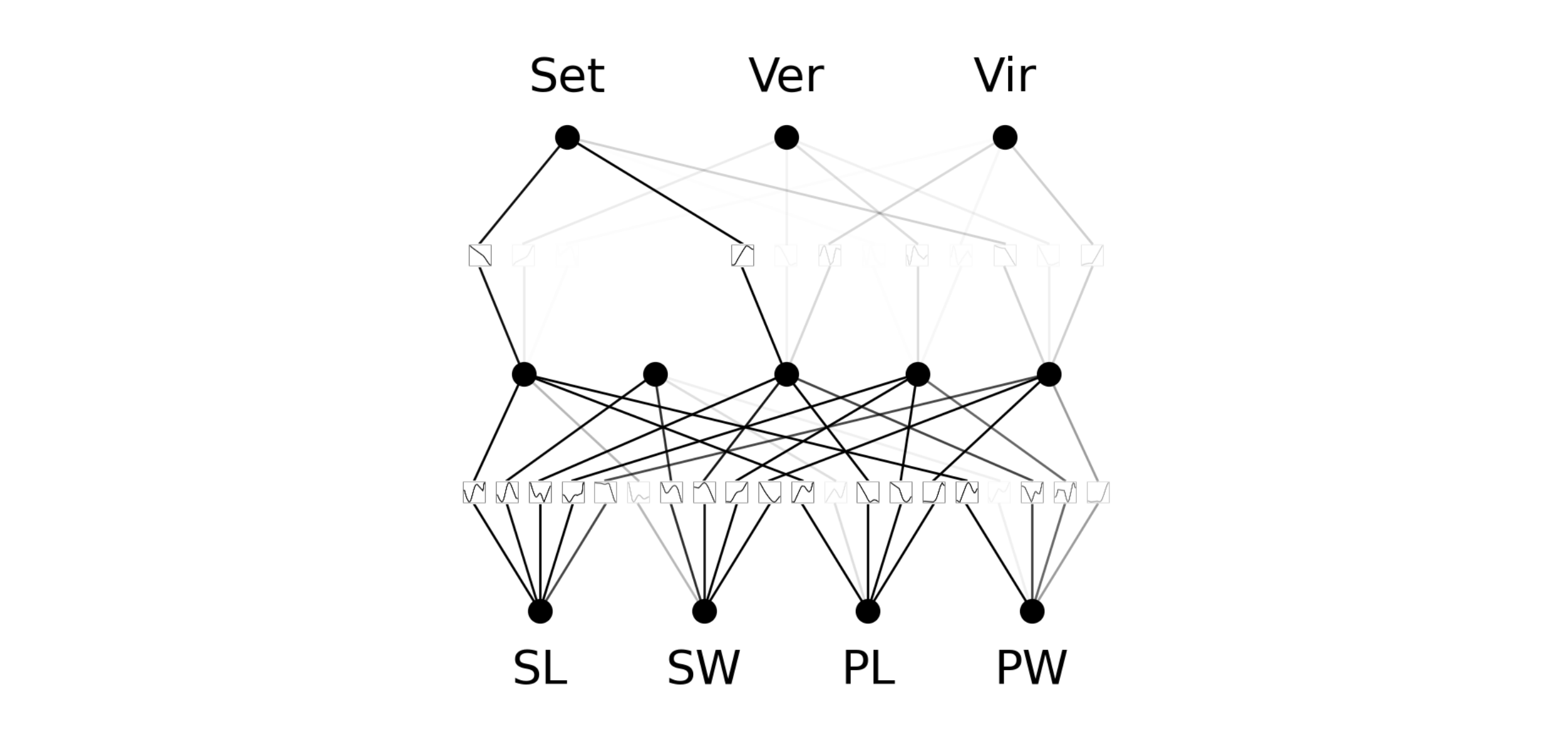
Tuyệt vời! Vậy là chúng ta đã có một mô hình KAN đơn giản và có thể quan sát tất cả các B-spline được khởi tạo trên các cạnh giữa các nơ-ron. Trong ví dụ này, bốn biến ở phía dưới biểu diễn đầu vào của bộ dữ liệu Iris (chiều dài đài hoa, chiều rộng đài hoa, chiều dài cánh hoa và chiều rộng cánh hoa), còn ba biến ở phía trên là ba loại hoa iris khác nhau mà chúng ta đang cố dự đoán.
Bây giờ, hãy huấn luyện KAN này. Quá trình huấn luyện có thể thực hiện tương tự như một mạng nơ-ron tiêu chuẩn, bằng cách sử dụng:
- Một trình tối ưu hóa (optimizer),
- Một hàm mất mát (loss function),
- Một số lượng epochs (vòng lặp huấn luyện),
- Và đặc biệt, các tham số phạt (penalty parameters) - điều này sẽ không được giải thích chi tiết trong bài viết này.

  
def train_acc():
    return torch.mean((torch.argmax(model(iris_dataset['train_input']), dim=1) == iris_dataset['train_label']).float())

def test_acc():
    return torch.mean((torch.argmax(model(iris_dataset['test_input']), dim=1) == iris_dataset['test_label']).float())

results = model.fit(iris_dataset, opt="Adam", metrics=(train_acc, test_acc),
                      loss_fn=torch.nn.CrossEntropyLoss(), steps=100, lamb=0.01, lamb_entropy=10., save_fig=True, img_folder=image_folder)
print(results['train_acc'][-1], results['test_acc'][-1])

(0.9916667342185974, 1.0)

Chúng ta sẽ sử dụng thụât toán Adam để tối ưu, CrossEntropyLoss làm hàm mất mát (vì chúng ta đang thực hiện phân loại đa lớp), và huấn luyện trong 100 epochs. Quá trình này mất khoảng 8.5 phút để huấn luyện và chúng ta đạt được độ chính xác trên tập huấn luyện và tập kiểm tra lần lượt là (0.992, 0.934). Chúng ta có thể đồng ý rằng điều này rõ ràng là rất thành công! Hãy xem cách các B-spline đã biến đổi trong quá trình huấn luyện.

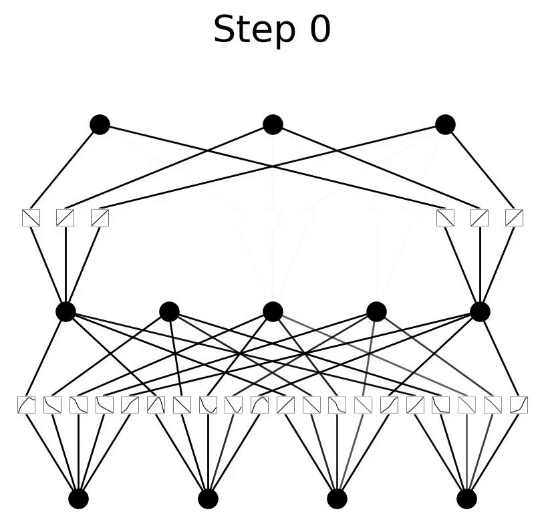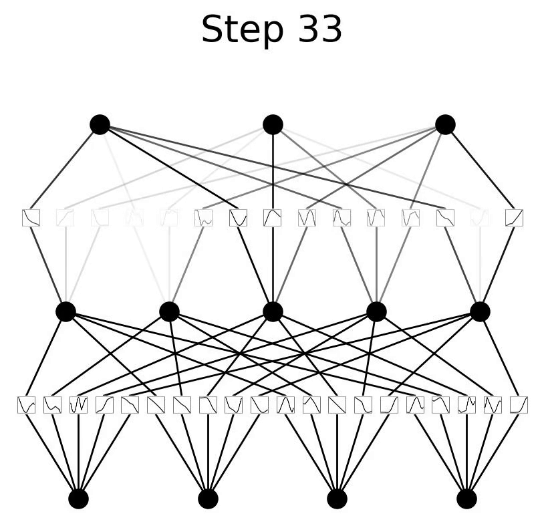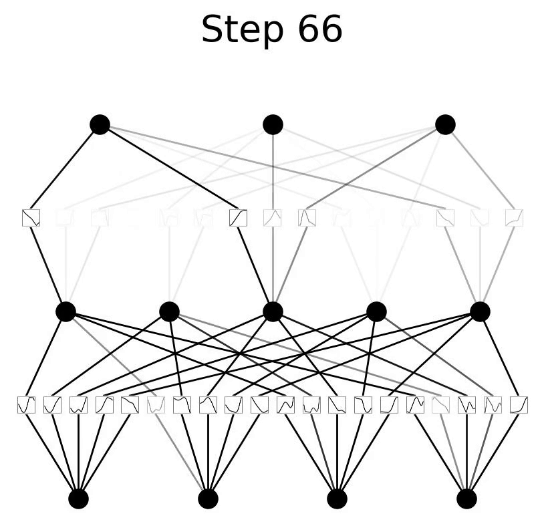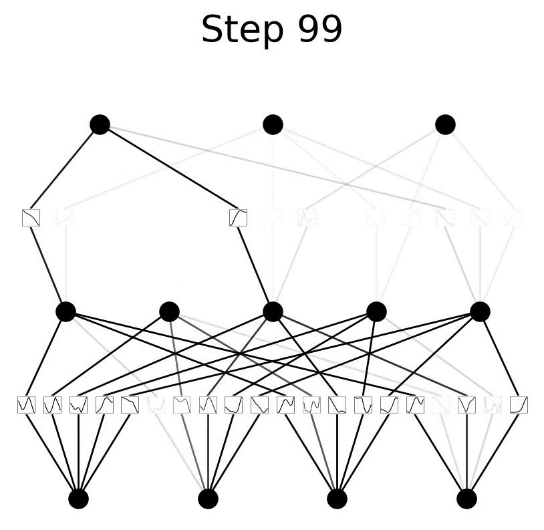
Trong những epoch đầu, các b-splines thay đổi rất nhiều cho đến khi cuối cùng hội tụ thành một hình dạng ổn định. Hãy xem KAN của chúng ta trông như thế nào bây giờ.

Điều này thật thú vị, một số cạnh đã biến mất hoàn toàn ?! Tôi sẽ không đi vào chi tiết đầy đủ vì điều đó là không cần thiết, nhưng các nơ-ron có hoạt động dưới một ngưỡng nhất định sẽ bị tắt hoàn toàn để giúp mạng hoạt động hiệu quả hơn. Chúng ta có thể cắt đi những cạnh để loại bỏ đi nhưng node không hoạt động. Đoạn code dưới đây giúp làm điều đó:

  
model = model.prune()

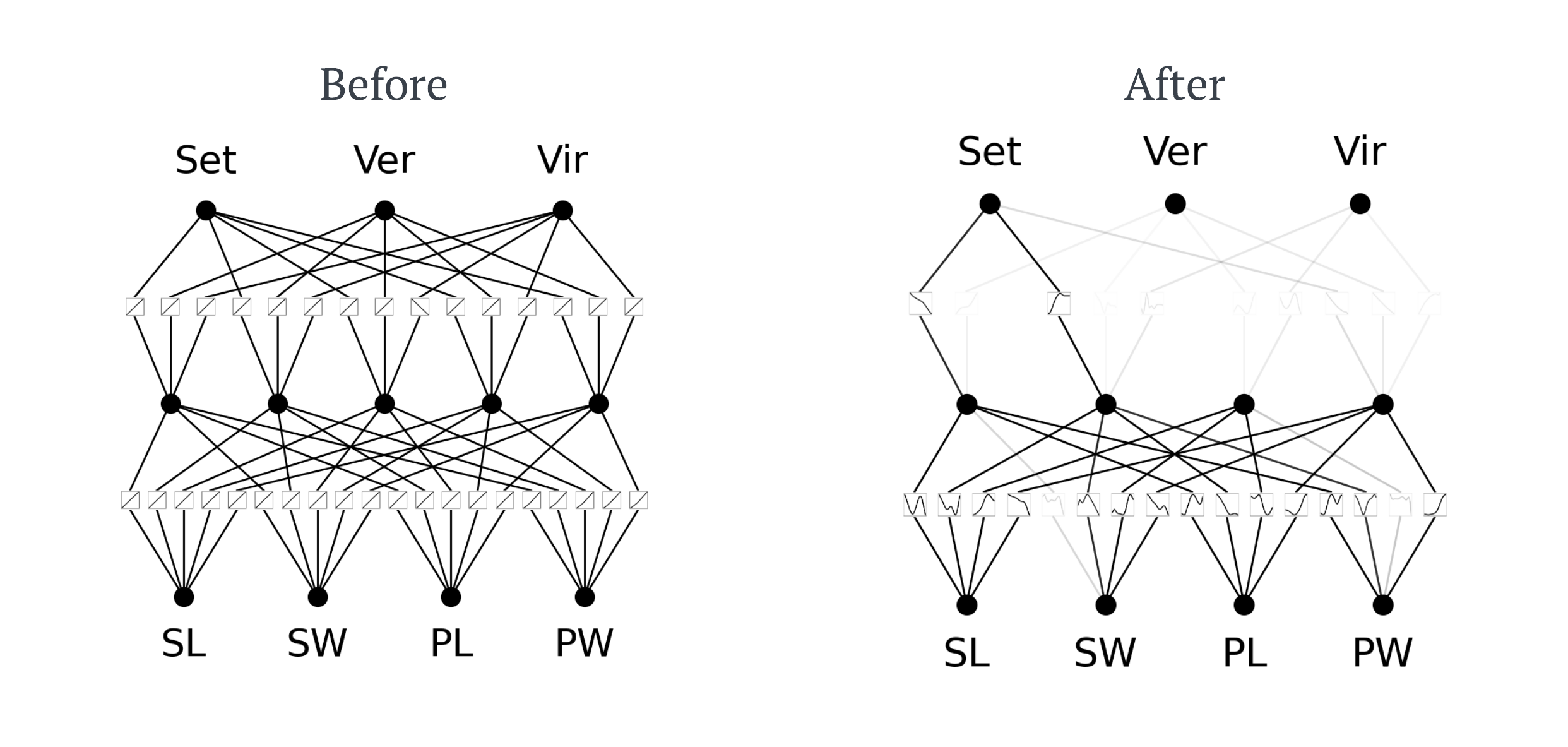
Giờ hãy nhìn xem mô hình KAN bây giờ trông như thế nào:

Như bạn có thể thấy, lớp ẩn gồm 5 nút đã được giảm xuống còn 4 giúp KAN tính toán hiệu quả hơn mà không làm giảm độ chính xác. Bây giờ chúng ta có thể fine-tune lại mô hình KAN này, lần này chỉ 50 epoch và đạt được độ chính xác huấn luyện và kiểm tra tương ứng là (1.0, 1.0).

  
# fine tune
results_1 = model.fit(iris_dataset, opt="Adam", metrics=(train_acc, test_acc),
                      loss_fn=torch.nn.CrossEntropyLoss(), steps=50, lamb=0.01, lamb_entropy=10.)
print(results_1['train_acc'][-1], results_1['test_acc'][-1])

(1.0, 1.0)

Chúng ta đã xây dựng, huấn luyện, cắt tỉa và fine-tune KAN.Mặc dù đây là một mô hình nhỏ nhưng nó cho thấy KAN thực sự có sức mạnh như thế nào. Trước khi so sánh chúng với MLP truyền thống như thế nào, tôi muốn cho bạn thấy cái hay nhất của KAN ngay sau đây.
Bây giờ chúng ta có thể trích xuất công thức ký hiệu của KAN. Điều này có ý nghĩa hơn nếu tôi chỉ cho bạn thấy. Ví dụ: lấy lớp đầu tiên (Setosa) mà tôi đang cố gắng dự đoán. Công thức ký hiệu mà KAN đã học cho lớp này là:

  
lib = ['x','x^2','x^3','x^4','exp','log','sqrt','tanh','sin','tan','abs']
model.auto_symbolic(lib=lib)
formula1, formula2, formula3 = model.symbolic_formula()[0]
print(formula1)

\[1.61 \left( -\sin(0.55x_3 + 9.34) + 0.12\tan(0.57x_1 \dots \right)\]

Chúng ta có thể làm được rất nhiều điều với công thức này. Nếu chúng ta lấy công thức để tính kết quả đầu ra, nghĩa là một lần nữa chúng ta tiết kiệm được rất nhiều tính toán. Vì đây là công thức tương tự mà mạng sử dụng nên chúng ta sẽ không mất bất kỳ độ chính xác nào khi suy ra điều này thay vì mạng. Thật tuyệt phải không !

So sánh với Neural Networks

Các tác giả của KAN đã có những lời phát biểu khá là tự tin khi nói rằng KAN sẽ thay thế MLP. Bây giờ chúng ta sẽ hãy làm thử một so sánh nhỏ, chúng ta sẽ tạo một mạng MLP có kiến trúc y hệt như sau:

  
class IrisNet(nn.Module):
    def __init__(self):
        super(IrisNet, self).__init__()
        self.fc1 = nn.Linear(4, 5)  # 4 inputs to 5 hidden nodes
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(5, 3)  # 5 hidden nodes to 3 outputs

    def forward(self, x):
        x = self.fc1(x)
        x = self.relu(x)
        x = self.fc2(x)
        return x

Chúng ta cũng sẽ dùng cùng một thụât toán tối ưu, cùng số epoch. Bảng dưới đây là kết quả so sánh:

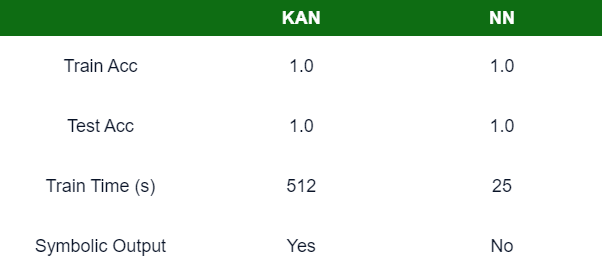
Cả hai mô hình đều có thể đạt được độ chính xác cao, thực sự là độ chính xác hoàn hảo. Một so sánh chính là thời gian đào tạo, MLP chỉ yêu cầu một phần thời gian đào tạo cần thiết. Những thử nghiệm này chỉ được thực hiện trên các kiến trúc nhỏ. Khi tôi tăng kích thước mô hình KAN, thời gian đào tạo mất ~30 phút trên GPU. Tuy nhiên, KAN có thể cung cấp các công thức ký hiệu cho các đặc trưng đã học, còn MLP thì không thể.
Dưới đây là bảng so sánh khi được train trên dữ liệu dự đoán giá nhà tại California:

Có thể đối với các bộ data nhỏ như trên, mô hình KAN hoạt động tốt hơn MLP. Nhưng thời gian huấn luyện của KAN quá lâu. Điều này dẫn đến một nghi vấn là nếu như MLPđược huấn luyện lâu như mô hình KAN thì có thể MLP sẽ đạt độ chính xác bằng hoặc thậm chí là tốt hơn KAN.

Tại sao lại dùng KAN

Cho đến nay, chúng ta đã thấy rằng KAN có thể đạt độ chính xác tốt hơn so với MLP (trong một số trường hợp), và xuất ra công thức biểu tượng, nhưng với chi phí huấn luyện cực kỳ chậm. Vậy tại sao lại sử dụng KAN thay vì MLP? Dưới đây là những suy nghĩ của tôi về các ứng dụng:
- Ứng dụng di động: Các mạng dự đoán gặp khó khăn trong việc cân bằng giữa độ chính xác cao và tính toán ít, do tài nguyên tính toán hạn chế trên điện thoại. Tôi cảm thấy KAN sẽ phát huy ưu thế ở đây vì chúng có thể đạt được độ chính xác cao, sau đó ta có thể chuyển đổi mạng thành một công thức biểu tượng. Rõ ràng, suy luận có thể được thực hiện trên công thức này thay vì mạng đắt tiền.
- Nhiệm vụ liên quan đến khoa học: Một nhiệm vụ khoa học, chẳng hạn như điều chỉnh các phương trình vật lý hoặc giải phương trình vi phân (PDE), sẽ rất lý tưởng.
- Khả năng giải thích: Trong những trường hợp hiếm hoi, khi khả năng giải thích là yếu tố quan trọng hơn các yếu tố khác, KANsẽ là lựa chọn lý tưởng thay vì các phương pháp giải thích hiện tại trong MLP, như SHAP hoặc giá trị LIME.
Hiện tại, cá nhân tôi cảm thấy rằng các trường hợp sử dụng vẫn còn hạn chế. Nếu có thể khắc phục được một số hạn chế của KAN, chẳng hạn như tốc độ huấn luyện chậm và sự không ổn định, thì chúng sẽ có nhiều ứng dụng hơn.

3. Tổng Kết

Mạng Kolmogorov-Arnold (KAN) mang đến một sự thay thế độc đáo cho các mạng nơ-ron truyền thống. Trong bài viết blog này, chúng ta đã khám phá ra rằng mặc dù KAN có tiềm năng đạt độ chính xác cao hơn và cung cấp những lợi thế độc đáo như đại diện biểu tượng của các hàm học được, chúng cũng đi kèm với những đánh đổi đáng kể. Một trong những yếu tố nổi bật trong đó là thời gian huấn luyện dài, điều này có thể là yếu tố quan trọng đối với các ứng dụng thực tế. Mặc dù vậy, KAN mang đến những triển vọng thú vị cho nghiên cứu và phát triển trong tương lai.
Nếu bạn vẫn còn mơ hồ với các công thức, tôi rất khuyến khích bạn nên xem hai video cực kỳ dễ hiểu này:
1. Kolmogorov-Arnold Networks (KANs) - What are they and how do they work?
2. The Kolmogorov-Arnold Theorem

4. Tài liệu tham khảo

Blog trên là phiên bản được tôi dịch qua blog gốc sau: Demystifying Kolmogorov-Arnold Networks: A Beginner-Friendly Guide with Code
Rất cảm ơn anh Daniel Bethell vì có một bài viết thực sự chất lượng.

AI Research

kan

This post is licensed under CC BY 4.0 by the author.