Post

Xác Suất Thống Kê

Posted Updated
By Bui Quang Dat
35 min read
Xác Suất Thống Kê

Xác suất thống kê là nền tảng cốt lỏi trong machine learning, giúp chúng ta hiểu và xử lý dữ liệu một cách có hệ thống. Từ việc dự đoán khả năng xảy ra của một sự kiện, tối việc phân tích mối quan hệ giữa các biến số, xác suất thống kê giúp các mô hình machine learning trở nên chính xác và tin cậy hơn. Trong bài viết này, chúng ta sẽ khám phá các nguyên lý cơ bản về xác suất thống kê và vai trò của nó trong việc xây dựng các ứng dụng machine learning hiện đại.

1. Thống kê

Sự thật thì cứng đầu, còn thống kê thì mềm dẻo.

  • Mark Twain
  • Thống kê đề cập đến toán học và kỹ thuật mà chúng ta hiểu dữ liệu. Đó là một lĩnh vực phong phú, rộng lớn, phù hợp hơn với một kệ (hoặc phòng) trong thư viện hơn là một chương trong blog, và vì vậy chương này sẽ không nói hết được chi tiết về tất cả mọi thứ trong thống kê. Thay vào đó, tôi sẽ cố gắng dạy bạn vừa đủ để trở nên nguy hiểm, và khơi dậy sự quan tâm của bạn vừa đủ để bạn sẽ đi và học hỏi nhiều hơn.

Miêu tả bộ dữ liệu

  • Hãy tưởng tượng bạn là một CEO của một công ty và bạn muốn mời cả những người bạn bè của nhân viên đến để ăn mừng tiệc. Một cách đơn giản để mô tả dữ liệu đó chính là sử dụng mảng một chiều như sau (nhân viên 1 mời 100 bạn bè, nhân viên 2 mời 49 bạn bè):
1
2
3

num_friends = [100,49,41,40,25,21,21,19,19,18,18,16,15,15,15,15,14,14,13,13,13,13,12,12,11,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,8,8,8,8,8,8,8,8,8,8,8,8,8,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]

# Rất nhiều thành viên... (204 thành viên)
  • Đối với một tập dữ liệu đủ nhỏ, đây thậm chí có thể là mô tả tốt nhất. Nhưng đối với một tập dữ liệu lớn hơn, điều này là khó sử dụng và có thể không rõ ràng. (Hãy tưởng tượng bạn nhìn chằm chằm vào một danh sách 1 triệu con số.) Vì lý do đó, chúng ta sử dụng số liệu thống kê để chắt lọc và truyền đạt các tính năng có liên quan của dữ liệu.
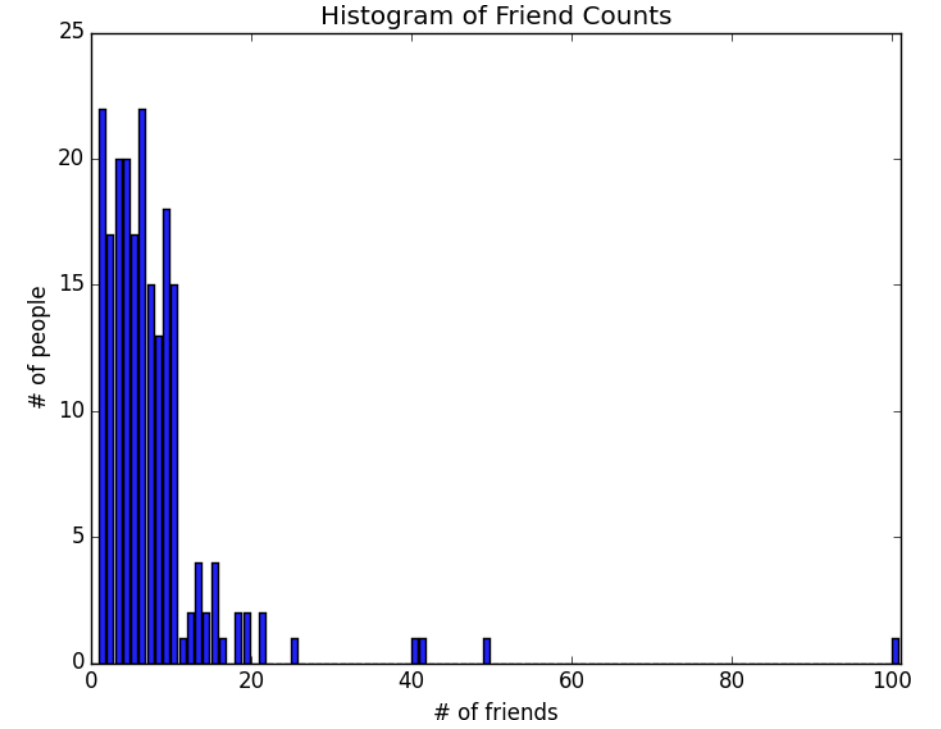
  • Cách tiếp cận đầu tiên là bạn sẽ tạo ra biểu đề cột để mô tả số lượng các thành viên có cùng số bạn bè bằng cách sử dụng Counter và plt.bar():
1
2
3
4
5
6
7
8
9
10
11
12

from collections import Counter
import matplotlib.pyplot as plt

friend_counts = Counter(num_friends)
xs = range(101)                         # largest value is 100
ys = [friend_counts[x] for x in xs]     # height is just # of friends
plt.bar(xs, ys)
plt.axis([0, 101, 0, 25])
plt.title("Histogram of Friend Counts")
plt.xlabel("# of friends")
plt.ylabel("# of people")
plt.show()

anh

  • Thật không may, biểu đồ trên vẫn khá khó để phân tích điều gì. Vậy nên bạn bắt đầu tạo ra một số thống kê. Cách đơn giản nhất là xem có bao nhiêu bạn bè của nhân viên:
1

num_points = len(num_friends) # 204
  • Bạn có thể quan tâm đến giá trị lớn nhất và nhỏ nhất:
1
2

largest_value = max(num_friends)  # 100
smallest_value = min(num_friends) # 1
  • Hoặc là bạn muốn quan tâm đến giá trị ở một vị trí nào đó:
1
2
3
4

sorted_values = sorted(num_friends)
smallest_value = sorted_values[0]           # 1
second_smallest_value = sorted_values[1]    # 1
second_largest_value = sorted_values[-2]    # 49

Xu hướng trung tâm (Central Tendencies)

  • Thông thường, chúng ta muốn quan tâm dữ liệu ở trung tâm như thế nào. Cách phổ biến nhất là sử dụng giá trị trung bình (mean hoặc average), tính bằng cách lấy tổng dữ liệu chia cho số lượng dữ liệu:
1
2
3

def mean(x):
  return sum(x) / len(x)
mean(num_friends) # 7.33333

  • Nếu bạn chỉ có hai điểm dữ liệu, giá trị trung bình chỉ đơn giản là điểm dữ liệu nằm giữa chúng. Khi bạn thêm nhiều điểm, giá trị trung bình sẽ thay đổi xung quanh, nhưng nó luôn phụ thuộc vào giá trị của mỗi điểm.

  • Đôi khi chúng ta cũng sẽ quan tâm đến giá trị trung vị (median), là giá trị ở giữa (nếu số điểm dữ liệu là lẻ) hoặc giá trị trung bình của hai giá trị ở giữa (nếu số điểm dữ liệu là chẵn).

  • Ví dụ: nếu chúng ta có năm điểm dữ liệu trong một mảng x được sắp xếp, thì trung bình là x[5 // 2] hoặc x[2]. Nếu chúng ta có sáu điểm dữ liệu, chúng ta muốn trung bình của x[2] (điểm thứ ba) và x[3] (điểm thứ tư).

  • Lưu ý rằng—không giống như giá trị trung bình, trung vị không phụ thuộc vào mọi giá trị trong dữ liệu của bạn. Ví dụ: nếu bạn làm cho điểm lớn nhất lớn hơn (hoặc điểm nhỏ nhất nhỏ hơn), các điểm ở giữa vẫn không thay đổi, có nghĩa là trung vị vẫn thế.

  • Hàm median dưới đây phức tạp hơn hàm mean ở trên 1 chút, chủ yếu là do trường hợp chẵn:
1
2
3
4
5
6
7
8
9
10

def median(v):
    n = len(v)
    v = sorted(v)
    midpoint = n // 2
    if n % 2 == 1:
        return v[midpoint]
    else:
        lo = midpoint - 1 
        hi = midpoint
        return (v[lo] + v[hi]) / 2
  • Rõ ràng, giá trị mean đơn giản hơn để tính toán và nó thay đổi trơn tru khi dữ liệu của chúng ta thay đổi. Nếu chúng ta có $n$ điểm dữ liệu và một trong số chúng tăng lên một số lượng nhỏ $e$, thì mean sẽ tăng $\frac{e}{n}$. (Điều này làm cho mean với tất cả các loại thủ thuật giải tích.) Trong khi đó, để tìm median, chúng ta phải sắp xếp dữ liệu của mình. Và thay đổi một trong các điểm dữ liệu của chúng ta theo một lượng nhỏ $e$ có thể làm tăng trung vị bằng $e$, một số ít hơn e hoặc hoàn toàn không thay đổi gì cả (tùy thuộc vào phần còn lại của dữ liệu).

Trên thực tế, có những thủ thuật không rõ ràng để tính toán hiệu quả các median mà không cần sắp xếp dữ liệu. Tuy nhiên, chúng nằm ngoài phạm vi của blog này, vì vậy chúng ta phải sắp xếp dữ liệu.

  • Đồng thời, giá trị mean rất nhạy cảm với các outliners trong dữ liệu. Nếu người dùng thân thiện nhất của chúng ta có 200 bạn bè (thay vì 100), thì giá trị trung bình sẽ tăng lên 7,82, trong khi mức median sẽ giữ nguyên. Nếu các outliners có khả năng là dữ liệu xấu, thì giá trị trung bình đôi khi có thể khiến chúng ta gây hiểu lầm về dữ liệu. Ví dụ, câu chuyện thường được kể rằng vào giữa những năm 1980, chuyên ngành tại Đại học Bắc Carolina có mức lương khởi điểm trung bình cao nhất là địa lý, chủ yếu là do ngôi sao NBA (outlier) Michael Jordan.
  • Một khái quát hóa của trung vị là phân vị (quantile), đại diện cho giá trị nhỏ hơn một phần trăm nhất định của dữ liệu. (Giá trị trung vị đại diện cho giá trị nhỏ hơn 50% dữ liệu)
1
2
3
4
5
6
7
8

def quantile(x, p):
    """returns the pth-percentile value in x"""
    p_index = int(p * len(x))
    return sorted(x)[p_index]
quantile(num_friends, 0.10) # 1
quantile(num_friends, 0.25) # 3
quantile(num_friends, 0.75) # 9
quantile(num_friends, 0.90) # 13
  • Một giá trị ít phổ biến hơn đó chính là mode, hay là phần tử xuất hiện nhiều nhất:
1
2
3
4
5
6

def mode(x):
    """returns a list, might be more than one mode"""
    counts = Counter(x)
    max_count = max(counts.values())
    return [x_i for x_i, count in counts.items() if count == max_count]
mode(num_friends)
  • Nhưng giá trị phổ biến nhất mà mọi người hay sử dụng vẫn chỉ là mean.

Phân tán (Dispersion)

  • Phân tán (Dispersion) đề cập đến các thước đo mức độ phân tán dữ liệu. Thông thường, chúng là số liệu thống kê mà giá trị nếu gần bằng 0 có nghĩa là dữ liệu không trải rộng và nếu có giá trị lớn có nghĩa là dữ liệu rất trải rộng. Ví dụ, chúng ta có thể định nghĩa giá trị phân tán là phạm vi (range), hiểu đơn giản là lấy phần tử lớn nhất trừ đi phần tử nhỏ nhất:
1
2
3

def data_range(x):
    return max(x) - min(x)
data_range(num_friends) # 99
  • Phạm vi bằng 0 khi phần tử lớn nhất bằng phần tử nhỏ nhất, điều này xảy ra khi tất cả phần tử bằng nhau. Ngược lại, nếu phạm vi lớn, thì giá trị lớn nhất lớn hơn nhiều so với giá trị nhỏ nhất, suy ra dữ liệu trải rộng hơn.
  • Giống như median, range cũng không phụ thuộc vào hết tất cả dữ liệu mà chỉ phụ thuộc vào giá trị lớn nhất và nhỏ nhất.
  • Một thước đo dữ phân tán phức tạp hơn đó chính là phương sai (variance), được tính như sau:
1
2
3
4
5
6
7
8
9
10
11

def de_mean(x):
    x_bar = mean(x)
    return [x_i - x_bar for x_i in x]
def variance(x):
    n = len(x)
    deviations = de_mean(x)
    var = 0
    for x in deviations:
      var += x*x
    return var / (n-1)
variance(num_friends) # 81.54
  • Chúng ta sẽ xem tiếp thước đo nữa đó chính là độ lệnh chuẩn (standard deviation), được tính bằng căn bậc hai của phương sai:
1
2
3
4

import math
def standard_deviation(x):
    return math.sqrt(variance(x))
standard_deviation(num_friends) # 9.03
  • Cả range và standard deviation đều nhạy cảm với outliners giống như mean. Sử dụng ví dụ tương tự, nếu người dùng thân thiện nhất của chúng tôi có 200 bạn bè, độ lệch chuẩn sẽ là 14,89, cao hơn 60%! Một giải pháp thay thế tốt hơn sẽ tính toán sự khác biệt giữa giá trị phân vị thứ 75 và giá trị phân vị thứ 25:
1
2
3

def interquartile_range(x):
    return quantile(x, 0.75) - quantile(x, 0.25)
interquartile_range(num_friends) # 6
  • Hàm trên sẽ không bị ảnh hưởng nhiều bởi lượng nhỏ outliners.

Hệ số tương quan (Correlation)

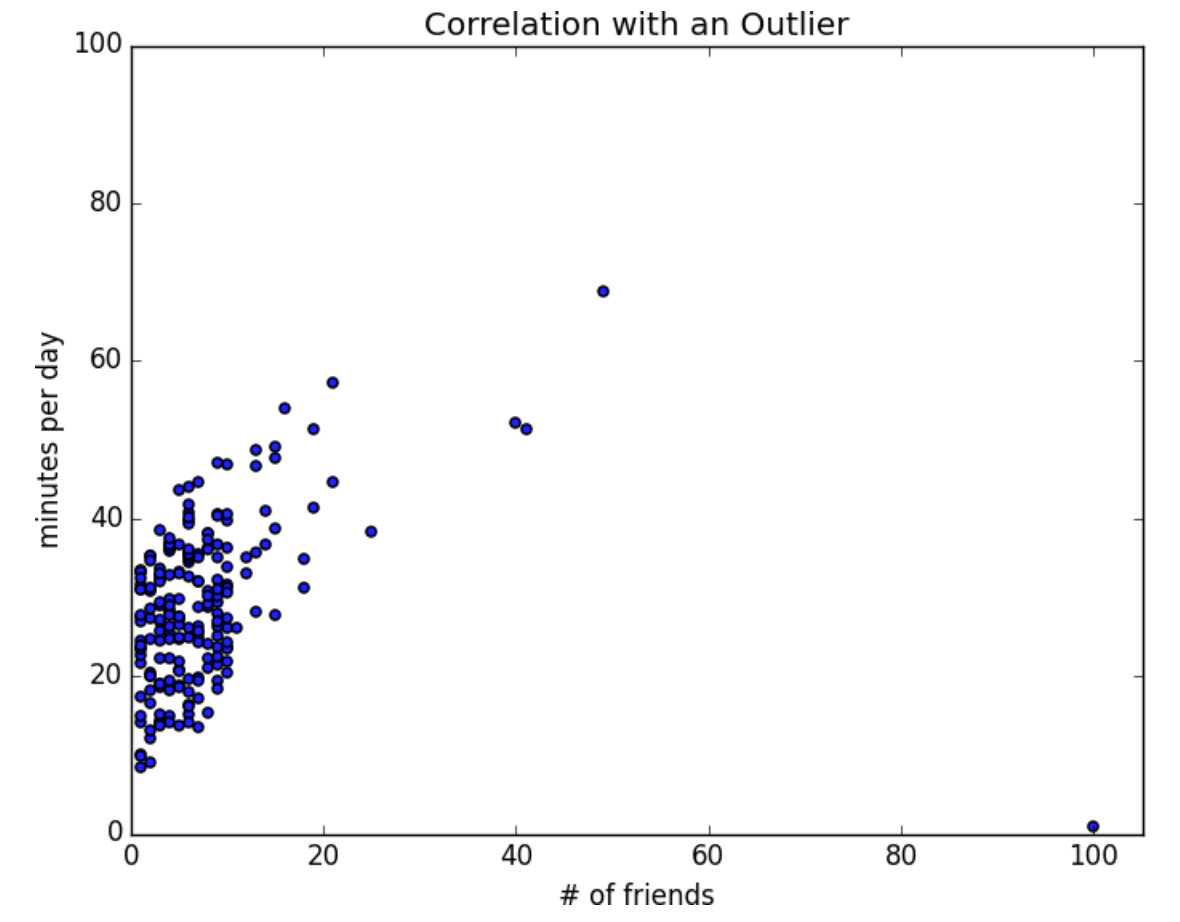
  • Bạn có một giả thuyết rằng lượng thời gian mà mọi người lướt facebook phụ thuộc vào số lượng bạn bè họ có trên facebook (càng nhiều bạn bè thì lượng thời gian lướt face càng nhiều). Làm thế nào để kiểm chứng điều này ?
  • Sau khi tìm hiểu qua nhật ký lưu lượng truy cập, bạn đã tính ra một danh sách daily_minutes cho biết mỗi người dùng dành bao nhiêu phút mỗi ngày trên facebook và bạn đã sắp xếp nó để các phần tử của nó tương ứng với các phần tử của danh sách num_friends. Bạn muốn điều tra mối quan hệ giữa hai chỉ số này.
1

daily_minutes = [1,68.77,51.25,52.08,38.36,44.54,57.13,51.4,41.42,31.22,34.76,54.01,38.79,47.59,49.1,27.66,41.03,36.73,48.65,28.12,46.62,35.57,32.98,35,26.07,23.77,39.73,40.57,31.65,31.21,36.32,20.45,21.93,26.02,27.34,23.49,46.94,30.5,33.8,24.23,21.4,27.94,32.24,40.57,25.07,19.42,22.39,18.42,46.96,23.72,26.41,26.97,36.76,40.32,35.02,29.47,30.2,31,38.11,38.18,36.31,21.03,30.86,36.07,28.66,29.08,37.28,15.28,24.17,22.31,30.17,25.53,19.85,35.37,44.6,17.23,13.47,26.33,35.02,32.09,24.81,19.33,28.77,24.26,31.98,25.73,24.86,16.28,34.51,15.23,39.72,40.8,26.06,35.76,34.76,16.13,44.04,18.03,19.65,32.62,35.59,39.43,14.18,35.24,40.13,41.82,35.45,36.07,43.67,24.61,20.9,21.9,18.79,27.61,27.21,26.61,29.77,20.59,27.53,13.82,33.2,25,33.1,36.65,18.63,14.87,22.2,36.81,25.53,24.62,26.25,18.21,28.08,19.42,29.79,32.8,35.99,28.32,27.79,35.88,29.06,36.28,14.1,36.63,37.49,26.9,18.58,38.48,24.48,18.95,33.55,14.24,29.04,32.51,25.63,22.22,19,32.73,15.16,13.9,27.2,32.01,29.27,33,13.74,20.42,27.32,18.23,35.35,28.48,9.08,24.62,20.12,35.26,19.92,31.02,16.49,12.16,30.7,31.22,34.65,13.13,27.51,33.2,31.57,14.1,33.42,17.44,10.12,24.42,9.82,23.39,30.93,15.03,21.67,31.09,33.29,22.61,26.89,23.48,8.38,27.81,32.35,23.84]
  • Trước tiên, chúng ta sẽ xem xét hiệp phương sai (covariance), bạn có thể coi như nó là ghép đôi của phương sai. Trong khi phương sai đo lường cách một biến duy nhất lệch so với giá trị trung bình của nó, hiệp phương sai đo lường cách hai biến thay đổi song song với giá trị trung bình của chúng:
1
2
3
4
5
6
7
8
9
10
11

def dot(x,y):
  assert len(x) == len(y)
  w = 0
  for i in range(len(x)):
    w += x[i]*y[i]
  return w

def covariance(x, y):
    n = len(x)
    return dot(de_mean(x), de_mean(y)) / (n - 1)
covariance(num_friends, daily_minutes) # 22.43

  • Để ý rằng hàm dot sẽ là tổng các tích của hai phần tử tương ứng trong hai mảng (giống như phép tích vô hướng hai vector). Khi một phần tử trong x nhỏ hơn giá trị mean thì phần tử đó trong de_mean(x) sẽ có giá trị âm và ngược lại, nếu như phần tử trong x mà lớn hơn mean thì phần tử đó trong de_mean(x) sẽ có giá trị dương (vì de_mean(x) tính bằng cách lấy x trừ đi mean). Vậy nên, nếu cặp giá trị tương ứng trong x và y đều nhỏ hơn mean thì cặp giá trị tương ứng trong de_mean(x) và de_mean(y) đều âm, nhưng hai số âm nhân vào nhau sẽ thành số dương, vậy nên phép tính dot càng lớn (vì được cộng vào một số dương), nên hiệp phương sai càng lớn. Tương tự nếu cặp giá trị tương ứng trong x và y đều lớn hơn mean thì phép tính dot càng lớn, hiệp phương sai càng lớn. Nếu như mà một trong hai cặp trong x và y mà một đứa lớn hơn mean, một đứa nhỏ hơn mean thì dot sẽ phải cộng một số âm, nên dot sẽ bé dẫn đến hiệp phương sai cũng sẽ bé. Vậy nên, nếu hiệp phương sai giữa x và y lớn có nghĩa là x tăng thì y cũng sẽ có xu hướng tăng, x giảm thì y cũng sẽ có xu hướng giảm. Còn hiệp phương sai mà bé thì người lại, x tăng thì y giảm, x giảm thì y tăng. Nếu hiệp phương sai gần bằng 0 thì có nghĩa là x và y chả có sự liên quan gì với nhau.

  • Nhưng thực thế, dựa vào hiệp phương sai thì chúng ta rất khó để kết luận điều gì. Lấy một ví dụ,nếu như mỗi người dùng đều có gấp đôi số bạn bè nhưng thời gian lướt facebook vẫn thế. Trong trường hợp đó thì hiệp phương sai của chúng ta đã lớn gấp đôi nhưng thực chất mối quan hệ của hai biến đó không khác gì trước khi chúng ta thay đổi cả. Vì lý do này, người ta thường tính hệ số tương quan (correlation), bằng cách lấy hiệp phương sai chia cho độ lệch chuẩn của cả hai biến:

1
2
3
4
5
6
7
8

def correlation(x, y):
    stdev_x = standard_deviation(x)
    stdev_y = standard_deviation(y)
    if stdev_x > 0 and stdev_y > 0:
        return covariance(x, y) / stdev_x / stdev_y
    else:
        return 0 # if no variation, correlation is zero
correlation(num_friends, daily_minutes) # 0.25

  • Hệ số tương quan là một số thuộc từ -1 (hai biến trái ngược nhau hoàn toàn) đến 1 (hai biến có sự tương quan hoàn toàn). Một số như 0.25 có thể kết luận là có một chút sự tương quan của hai biến, nhưng không cao.

  • Hãy xem qua dữ liệu của ta một chút:

anh

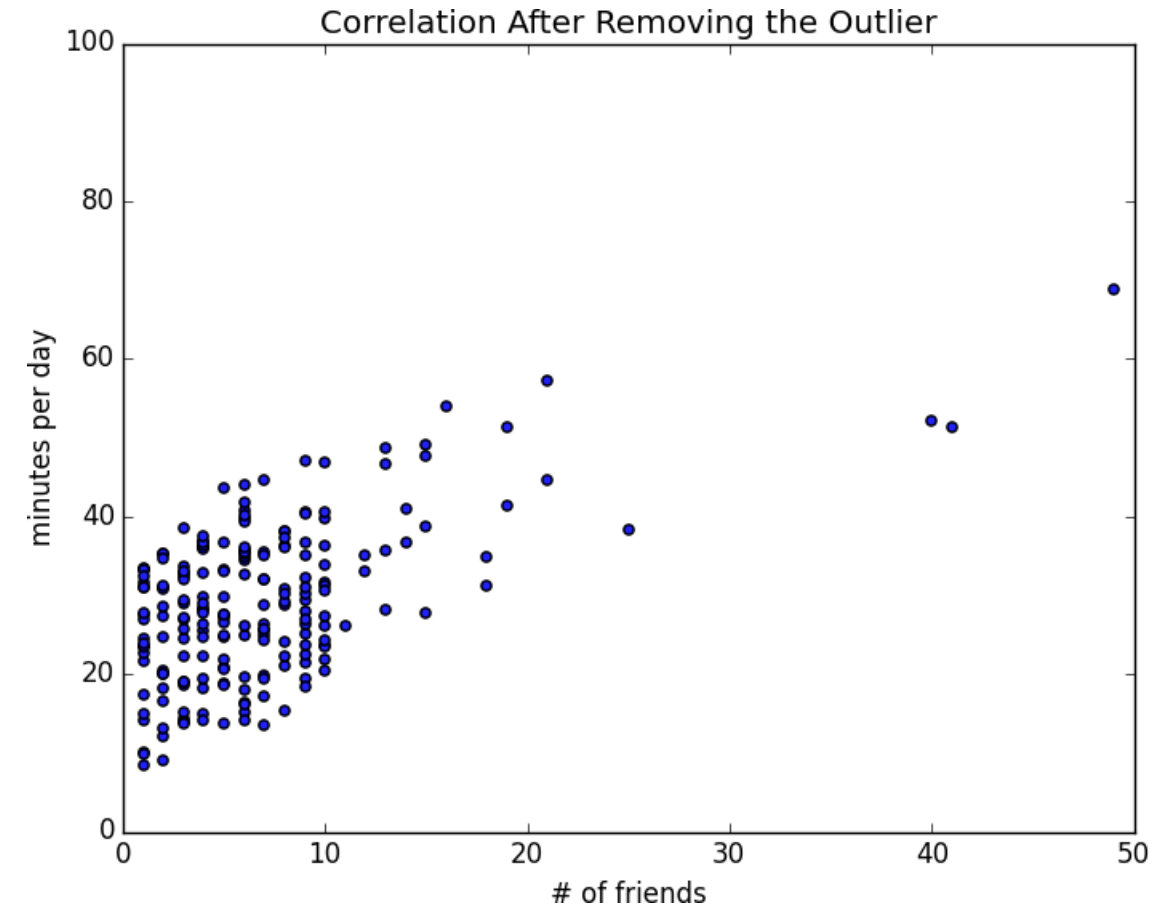
  • Có một người có 100 bạn bè nhưng chỉ dành 1 phút mỗi ngày lướt facebook, đây là một outlineer, và hệ số tương quan rất nhạy cảm với outliners. Chuyện gì xảy ra nếu chúng ta loại bỏ người đó:
1
2
3
4
5
6
7
8

outlier = num_friends.index(100) # index of outlier
num_friends_good = [x
                    for i, x in enumerate(num_friends)
                    if i != outlier]
daily_minutes_good = [x
                    for i, x in enumerate(daily_minutes)
                    if i != outlier]
correlation(num_friends_good, daily_minutes_good) # 0.57
  • Không có outliner, hệ số tương quan lớn hơn rất nhiều.

anh

Ngịch Lý Simpson (Simpson’s Paradox)

Một số điều cần lưu ý về hệ số tương quan

  • Hệ số tương quan bằng 0 chỉ ra rằng không có mối quan hệ tuyến tính giữa hai biến. Tuy nhiên, có thể có các loại mối quan hệ khác. Ví dụ: nếu:
1
2

x = [-2, -1, 0, 1, 2]
y = [ 2, 1, 0, 1, 2]
  • x và y có hệ số tương quan bằng 0. Nhưng chúng chắc chắn có một mối quan hệ – mỗi phần tử của y bằng giá trị tuyệt đối của phần tử tương ứng của x. Những gì x và y không có là một mối quan hệ trong đó biết $x_i$ so với trung bình (x) như thế nào cho chúng ta thông tin về cách $y_i$ so với trung bình (y). Đó là loại mối quan hệ mà hệ số tương quan tìm kiếm.
  • Ngoài ra, hệ số tương quan không cho bạn biết gì về mối quan hệ lớn như thế nào. Các biến:
1
2

x = [-2, 1, 0, 1, 2]
y = [99.98, 99.99, 100, 100.01, 100.02]
  • x và y có mối tương quan hoàn hảo, nhưng (tùy thuộc vào những gì bạn đang đo lường) rất có thể mối quan hệ này không thú vị lắm vì nó khá là hiển nhiên.

2. Xác Suất

  • Bạn nên nghĩ về xác suất như một cách để định lượng sự không chắc chắn liên quan đến các sự kiện được chọn từ một số sự kiện. Thay vì hiểu kỹ thuật về ý nghĩa của những thuật ngữ này, hãy nghĩ đến việc tung xúc xắc. Tập không gian mẫu bao gồm tất cả các kết quả có thể xảy ra. Và bất kỳ tập hợp con nào của những kết quả này đều là một sự kiện. Ví dụ: “xúc xắc tung ra một chấm” hoặc “xúc xắc tung một số chẵn”.
  • Về ký hiệu, chúng ta viết $P(E)$ tượng trưng cho “Xác suất của sự kiện $E$”.
  • Chúng ta sẽ sử dụng lý thuyết xác suất để xây dựng các mô hình. Chúng ta sẽ sử dụng lý thuyết xác suất để đánh giá các mô hình. Chúng ta sẽ sử dụng lý thuyết xác suất ở khắp mọi nơi.

Sự phụ thuộc và độc lập (Dependence and Independence)

  • Nói một cách đại khái, chúng ta nói rằng hai sự kiện $E$ và $F$ là phụ thuộc nếu sự kiện $E$ có xảy ra hay không phụ thuộc một phần vào sự kiện $F$, hoặc là sự kiện $F$ xảy ra phụ thuộc một phần vào sự kiện $E$. Ví dụ như hôm nay trời mưa thì khả năng tôi nghỉ học sẽ cao hơn là trời bình thường, thì sự kiện trời mưa và sự kiện tôi nghỉ học là hai sự kiện phụ thuộc. Hai sư kiện là độc lập nếu chúng không ảnh hưởng đến sự xảy ra của cả hai. Ví dụ ngày mai trời mưa và tung xúc sắc được 6 mặt là hai sự kiện độc lập vì chúng không liên quan đến nhau.

  • Một ví dụ khác là tung đồng xu. Sự kiện tung đồng xu được mặt ngửa ở lần thứ nhất và sự kiện tung đồng xu được mặt ngửa ở lần thứ hai là hai sự kiện độc lập, vì việc tung ngửa hay sấp ở lần thứ nhất không ảnh hưởng đến lần tung thứ hai. Nhưng sự kiện tung đồng xu được mặt ngửa ở lần thứ nhất và sự kiện tung đồng xu được mặt ngửa cả hai lần lại là phụ thuộc.
  • Về mặt toán học, chúng ta nói rằng hai sự kiện $E$ và $F$ là độc lập nếu xác suất cả hai đồng thời xảy ra băng tích xác suất của mỗi sự kiện xảy ra:
\[P(E,F) = P(E)P(F)\]

Xác suất có điều kiện (Conditional Probability)

  • Khi hai sự kiện E và F là độc lập, thì theo định nghĩa, chúng ta có:
\[P(E,F) = P(E)P(F)\]
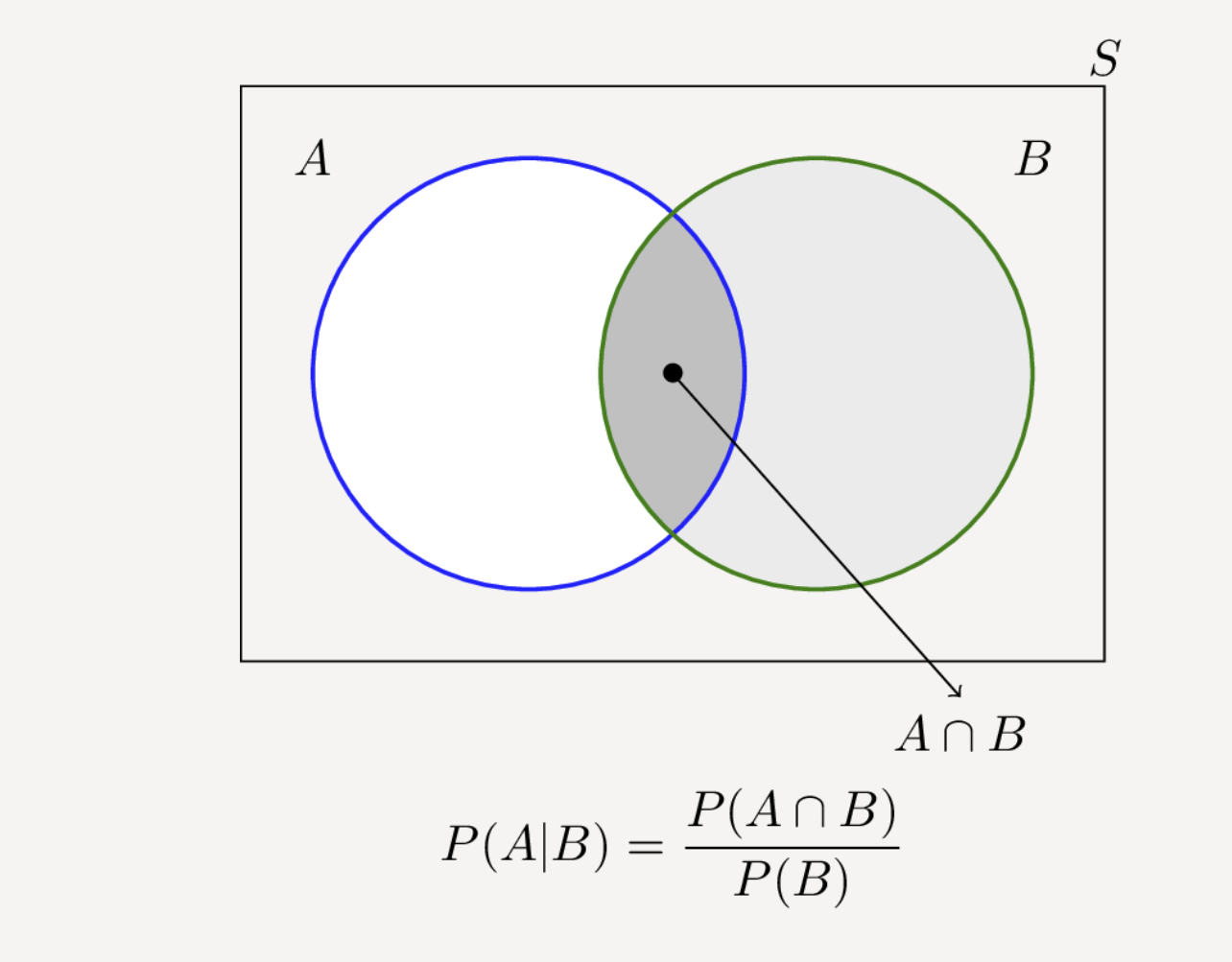
  • Nếu chúng không độc lập (và nếu xác suất của $F$ khác 0), thì chúng ta định nghĩa xác suất của $E$ với điều kiện $F$ là:
\[P(E|F) = \frac{P(E,F)}{P(F)}\]
  • Hiểu một cách đơn giản là sự kiện $F$ đã xảy ra rồi và bạn cần phải tính xác suất để sự kiện $E$ xảy ra. Nhìn vào biểu đồ ven dưới để hiểu rõ tại sao lại có công thức như trên:

anh

  • Chúng ta có thể viết lại công thức thành:
\[P(E,F) = P(E|F)P(E)\]
  • Khi $E$ và $F$ là độc lập, thì sẽ cho ta công thức sau:
\[P(E|F) = P(E)\]
  • Hiểu một cách đơn giản là, sự kiện $F$ xảy ra rồi thì cũng không ảnh hưởng đến xác suất xảy ra sự kiện $E$.
  • Một ví dụ khá là thú vị là có một gia đình có hai người con (chưa biết giới tính). Chúng ta có thể giả sử như sau:
    1. Mỗi người con có xác suất là con trai hoặc con gái như nhau (50-50)
    2. Giới tính người con thứ hai là độc lập với giới tính người con thứ nhất
  • Vậy sự kiện “Không có con gái” có xác xuất là $\frac{1}{4}$, sự kiện “Có một gái, một trai” có xác suất là $\frac{1}{2}$ và sự kiện “Cả hai đều là con gái” có xác suất là $\frac{1}{4}$
  • Vậy giờ xác suất của sự kiện “Cả hai là con gái” ($B$) khi đã biết sự kiện “Người con lớn tuổi hơn là con gái” ($G$) là bao nhiêu ? Sử dụng công thức ta có:
\[P(B|G) = \frac{P(B,G)}{P(G)} = \frac{P(B)}{P(G)} = \frac{1}{2}\]

Vì sự kiện $B$ và sự kiện $G$ (“Cả hai đều là con gái và người con lớn tuổi hơn là con gái”) chỉ là sự kiện $B$. (Khi bạn đã biết cả hai là con gái rồi thì hiển nhiên là người con lớn tuổi hơn là con gái).

  • Rất có thể kết quả trên đúng với trực giác của bạn. Giờ hãy thử tính xem xác suất xảy ra sự kiện “Cả hai đều là con gái” khi đã biết sự kiện “Ít nhất một người con là con gái” ($L$) (có thể có một con gái hoặc hai con gái). Thật ngạc nhiên, kết quả khác hoàn toàn ở trên.
  • Như chúng ta đã biết, sự kiện $B$ và sự kiện $L$ (“Cả hai người con là con gái và ít nhất một người con là con gái”) chỉ là sự kiện $B$. Do đó, chúng ta có:
\[P(B|L) = \frac{P(B,L)}{P(L)} = \frac{P(B)}{P(L)} = \frac{1}{3}\]

  • Tại sao điều này lại xảy ra ? Theo như kết quả trên thì nếu tất cả những gì bạn biết là ít nhất một trong những đứa con là con gái, thì khả năng gia đình có một con trai và một con gái cao gấp đôi so với cả hai con gái !

  • Chúng ta có thể kiểm tra bằng cách tạo thật nhiều hộ gia đình:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def random_kid():
    return random.choice(["boy", "girl"])
both_girls = 0
older_girl = 0
either_girl = 0
random.seed(0)
for _ in range(10000):
    younger = random_kid()
    older = random_kid()
    if older == "girl":
        older_girl += 1
    if older == "girl" and younger == "girl":
        both_girls += 1
    if older == "girl" or younger == "girl":
        either_girl += 1
print("P(both | older):", both_girls / older_girl) # 0.514 ~ 1/2
print("P(both | either): ", both_girls / either_girl) # 0.342 ~ 1/3

Định lý Bayes (Bayes’s Theorem)

  • Giả sử chúng ta cần tính $P(E|F)$ nhưng chúng ta chỉ có thông tin của $P(F|E)$. Sử dụng định nghĩa xác suất có điều kiện hai lần, ta có:
\[P(E|F) = \frac{P(E,F)}{P(F)} = \frac{P(F|E)P(E)}{P(F)}\]
  • Sự kiện $F$ có thể được chia thành hai sự kiện là “F và E” và “F và không phải E”. Chúng ta ký hiệu $\overline{E}$ cho “không phải E”, thì công thức có thể viết như sau:
\[P(F) = P(F,E) + P(F, \overline{E})\]
  • Vậy nên:
\[P(E|F) = \frac{P(F|E)P(E)}{P(F,E) + P(F, \overline{E})} = \frac{P(F|E)P(E)}{P(F|E)P(E) + P(F|\overline{E})P(\overline{E})}\]
  • Công thức trên chính là định lý Bayes. Định lý này thường được sử dụng để chứng minh tại sao các nhà khoa học dữ liệu thông minh hơn bác sĩ. Hãy tưởng tượng một căn bệnh nào đó ảnh hưởng đến 1 trong 10.000 người (tức cứ 10000 người thì có 1 người bị bệnh). Và hãy tưởng tượng rằng có một thí nghiệm về căn bệnh này cho kết quả chính xác (“bệnh” nếu bạn mắc bệnh, “không bệnh” nếu bạn không) lên đến 99%.
  • Xét nghiệm dương tính có nghĩa là gì? Hãy sử dụng $T$ cho sự kiện “xét nghiệm của bạn dương tính” và $D$ cho sự kiện “bạn mắc bệnh”. Sau đó, Định lý Bayes nói rằng xác suất bạn mắc bệnh, khi đã biết kết quả xét nghiệm của bạn là dương tính, là:
\[P(D|T) = \frac{P(T|D)P(D)}{P(T|D)P(D) + P(T|\overline{D})P(\overline{D})}\]
  • Chúng ta biết $P(T|D)$ có nghĩa là xác suất một người đã bị mắc bệnh có xét nghiệm là dương tính, là 0.99. $P(D)$ là xác suất mà một người nào đó bị bệnh là $\frac{1}{10000} = 0.0001$. $P(T|\overline{D})$ là xác suất một người không bị bệnh có xét nghiệm là dương tính, giả sử là 0.01. Và $P(\overline{D})$ là xác suất một người nào đó không bị bệnh là 0.9999. Thay vào công thức trên, ta tính được:
\[P(D|T) = 0.98 \%\]

  • Có nghĩa là, ít hơn 1% số người mà bị bệnh sau khi có xét nghiệm là dương tính. Mặc dù đây là một phép tính đơn giản cho một nhà khoa học dữ liệu, nhưng hầu hết các bác sĩ sẽ đoán rằng $P(D|T)$ có xấp xỉ 2.

  • Một cách trực quan hơn để thấy điều này là tưởng tượng dân số 1 triệu người. Bạn sẽ thầy 100 người trong số họ mắc bệnh và 99 trong số 100 người đó có kết quả xét nghiệm dương tính. Mặt khác, bạn sẽ thấy 999.900 người trong số họ không mắc bệnh và 9.999 trong số đó có kết quả xét nghiệm dương tính. Điều đó có nghĩa là bạn sẽ chỉ mong đợi 99 trong số (99 + 9999) người xét nghiệm dương tính thực sự mắc bệnh.

Biến ngẫu nhiên (Random Variable)

  • Biến ngẫu nhiên là một biến có các giá trị liên quan tới một phân phối xác suất. Một biến ngẫu nhiên rất đơn giản là biến bằng 1 nếu tung đồng xu ngửa, bằng 0 nếu tung đồng xu sấp. Phức tạp hơn thì có thể đo số lượng mặt ngửa khi tung đồng xu 10 lần hoặc là chọn ngẫu nhiên một số từ 1 đến 100. Hiểu đơn giản thì biến ngẫu nhiên là một giá trị ngẫu nhiên, được chọn từ một sự kiện nào đó.

  • Đôi khi chúng ta sẽ nói về giá trị kỳ vọng của một biến ngẫu nhiên, là giá trị trung bình của các giá trị của nó có trọng số theo xác suất của chúng, hay hiểu một cách đơn giản là lấy tổng các giá trị nhân với xác suất của giá trị đó. Biến lật đồng xu có giá trị kỳ vọng là $0.\frac{1}{2} + 1.\frac{1}{2} = \frac{1}{2}$ (Do tung đồng xu thì mình định nghĩa 0 là sấp, 1 là ngửa và sấp và ngửa đều có xác suất là $\frac{1}{2}$). Chọn ngẫu nhiên 1 số từ 1 đến 10 có giá trị kỳ vọng là 4.5.

  • Các biến ngẫu nhiên có thể được điều chỉnh theo các sự kiện giống như các sự kiện khác. Quay trở lại ví dụ hai đứa con từ, nếu $X$ là biến ngẫu nhiên đại diện cho số bé gái, $X$ bằng 0 với xác suất $\frac{1}{4}$, 1 với xác suất $\frac{1}{2}$ và 2 với xác suất $\frac{1}{4}$.
  • Chúng ta có thể định nghĩa một biến ngẫu nhiên mới $Y$ là số lượng bé gái với điều kiện là ít nhất một trong số các em là bé gái. Sau đó, $Y$ bằng 1 với xác suất $\frac{2}{3}$ và 2 với xác suất $\frac{1}{3}$ (đã tính ở trên). Và một biến $Z$ là số lượng bé gái với điều kiện là người con lớn hơn là con gái, $Z$ bằng 1 với xác suất $\frac{1}{2}$ và 2 với xác suất $\frac{1}{2}$.

Phân phối liên tục (Continuous Distributions)

  • Tung đồng xu tương ứng với một phân phối rời rạc - một phân phối liên kết xác suất dương với các kết quả rời rạc. Thường thì chúng ta sẽ muốn mô hình hóa các phân phối trên một chuỗi kết quả liên tục. (Đối với mục đích của tôi, những kết quả này sẽ luôn là số thực, mặc dù điều đó không phải lúc nào cũng đúng trong cuộc sống thực.) Ví dụ: phân phối đều đặt trọng số bằng nhau cho tất cả các số từ 0 đến 1.

  • Hiểu một cách đơn giản, biến liên tục là biến mà có giá trị thực. Ví dụ như bạn chọn ngẫu nhiên một số thực trong đoạn từ [0,1]. Nhưng bởi vì có vô số trong đoạn từ [0,1] nên gần như xác suất mà bạn chọn số nào đó là 0 (ví dụ như xác suất bạn chọn trúng số 0.23 trong vô vàn số trong đoạn [0,1] vậy). Vì lý do này, chúng ta biểu diễn một phân phối liên tục bằng hàm mật độ xác suất
  • Hàm mật độ xác suất (PDF - Probability Density Function) là một khái niệm trong xác suất và thống kê, dùng để mô tả mật độ xác suất của một biến ngẫu nhiên liên tục. Nó cho biết xác suất của một biến ngẫu nhiên liên tục rơi vào một giá trị hoặc một khoảng giá trị nào đó.
  • Hàm mật độ xác suất, ký hiệu $f(x)$, thỏa mãn các tính chất sau:
    1. $f(x) \geq 0$ với mọi $x$
    2. Tổng xác suất trên toàn không gian bằng 1:
\[\displaystyle \int_{-\infty}^{\infty}f(x)dx = 1\]
  1. Xác suất của biến ngẫu nhiên rơi vào một khoảng $[a,b]$ được tính bằng:
\[P(a \leq X \leq b) = \displaystyle \int_{a}^{b}f(x)dx\]

  • Lưu ý: Với biến ngẫu nhiên liên tục, giá trị tại một điểm cụ thể $P(X = x) = 0$. Xác suất chỉ được xác định thông qua một khoảng giá trị.

  • Hàm mật độ xác suất $f(x)$ cho biết “mức độ dày đặc” của xác suất tại một điểm $x$. Tuy nhiên, $f(x)$ không phải là xác suất thực sự, mà là mật độ.

  • Diện tích dưới đồ thị của hàm $f(x)$ rên một khoảng $[a,b]$ biểu diễn xác suất mà biến ngẫu nhiên nằm trong khoảng đó.

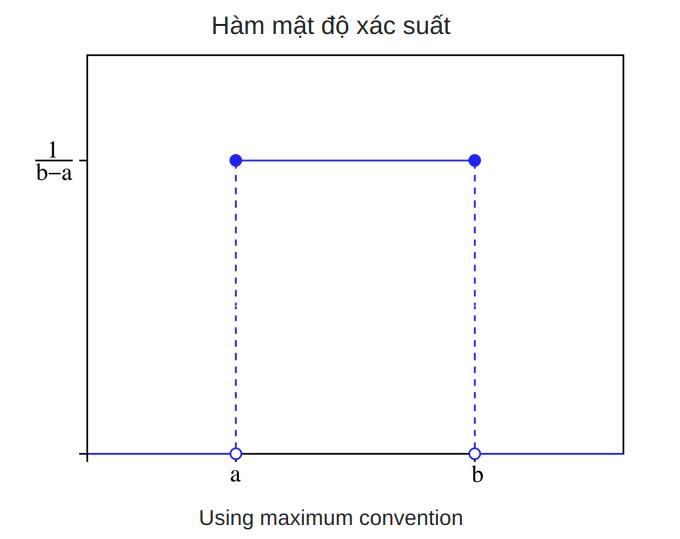
  • Phân phối đều liên tục (uniform distribution) là một phân phối mà xác suất xảy ra như nhau cho mọi kết cục của biến ngẫu nhiên liên tục. Phân phối đều liên tục đôi khi còn được gọi là phân phối hình chữ nhật và khi biểu diễn bằng hình vẽ sẽ có dạng hình chữ nhật.

anh

  • Hàm mật độ xác suất của một phân phối đều liên tục có dạng:
\[f(x) = \begin{cases} \frac{1}{b-a} & \text{nếu } a \leq x \leq b, \\ 0 & \text{ngược lại.} \end{cases}\]
  • Code của hàm mật độ xác suất trên đơn giản như sau:
    1
2

    def uniform_pdf(x,a,b):
  return 1 if x >= a and x <= b else 0
  • Chúng ta cũng thường hay nói đến hàm phân phối tích lũy. Hàm phân phối tích lũy (CDF - Cumulative Distribution Function) là một hàm dùng để mô tả xác suất tích lũy của một biến ngẫu nhiên, tức là xác suất biến ngẫu nhiên có giá trị nhỏ hơn hoặc bằng một giá trị nào đó.
  • Hàm phân phối tích lũy của một biến ngẫu nhiên $X$, ký hiệu là $F(x)$, được định nghĩa như sau với biến ngẫu nhiên liên tục:
\[F(x) = P(X \leq x) = \displaystyle \int_{-\infty}^{x}f(t)dt\]
  • Trong đó:
    • $f(t)$ là hàm mật độ xác suất (PDF - Probability Density Function).
    • $P(X \leq x)$ à xác suất biến ngẫu nhiên $X$ có giá trị nhỏ hơn hoặc bằng $x$.
  • Hàm phân bố tích lũy của một phân phối đều liên tục có dạng:
\[F(x) = \begin{cases} 0 & \text{nếu } x < a, \\ \frac{x-a}{b-a} & \text{nếu } a \leq x < b, \\ 1 & \text{nếu} x \geq b \end{cases}\]
  • Code hàm phân bố tích lũy của phân bố đều như sau:
1
2
3
4

def uniform_cdf(x,a,b):
    if x < a: return 0
    elif x >= a and x < b: return (x - a)/(b - a)
    else: return 1

Phân bố chuẩn (The Normal Distribution)

  • Phân phối chuẩn là vua của các phân phối. Nó là phân phối hình đường cong chuông cổ điển và được xác định hoàn toàn bởi hai tham số: giá trị trung bình $\mu$ (mean) và độ lệch chuẩn $\sigma$ (standard deviation). Giá trị trung bình cho biết vị trí của chuông và độ lệch chuẩn cho thấy mức độ “rộng” của nó.
  • Hàm mật độ xác suất (pdf) của phân bố chuẩn có công thức như sau:
\[f(x \mid \mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\]
  • Chúng ta có thể code như sau:
1
2
3
4

def normal_pdf(x, mu = 0, sigma = 1):
    sqrt_two_pi = math.sqrt(2 * math.pi)
    return (math.exp(-(x-mu) ** 2 / 2 / sigma ** 2) / (sqrt_two_pi * sigma))
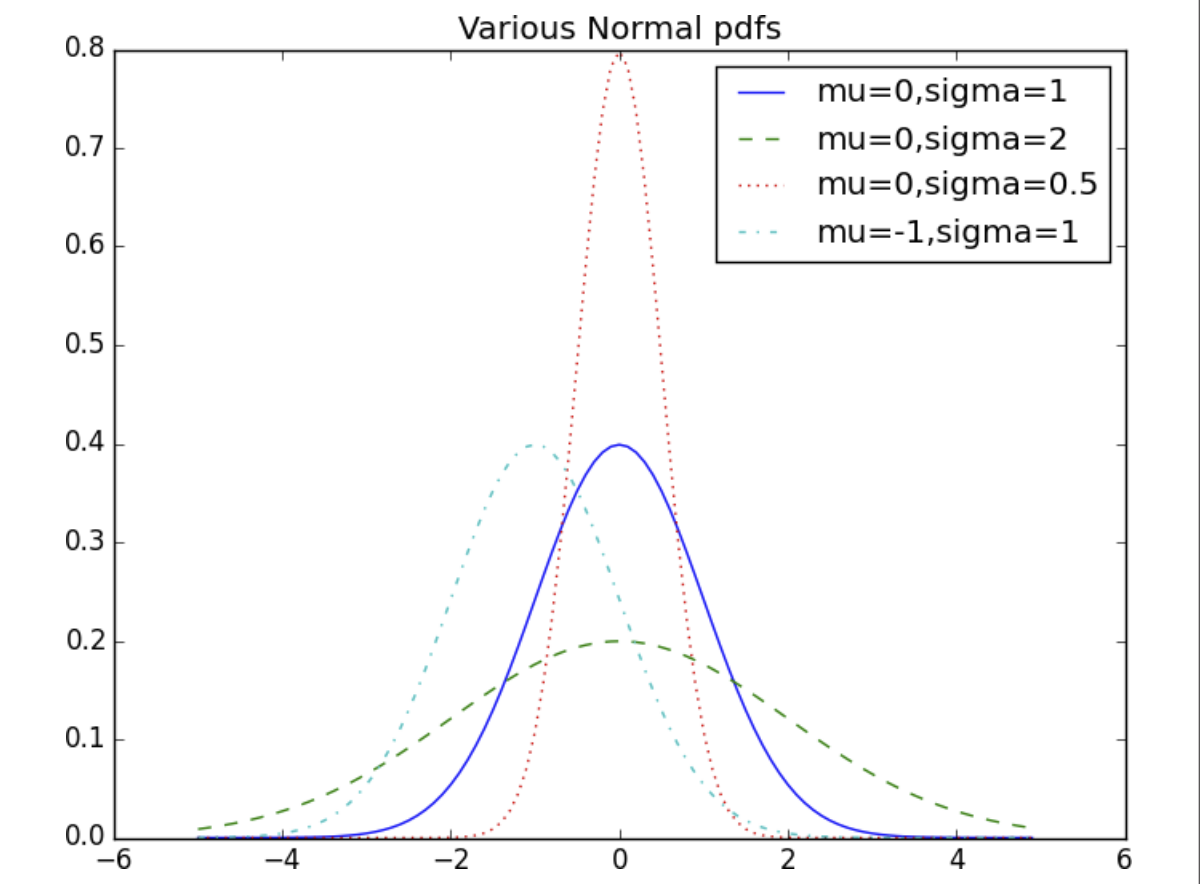
  • Ở hình dưới, chúng ta sẽ tạo các số từ -5 đến 5, mỗi số cách nhau 0.1 đơn vị và thử xem đồ thị phân bố chuẩn với các giá trị trung bình và độ lệch chuẩn khác nhau:
1
2
3
4
5
6
7
8

xs = [x / 10.0 for x in range(-50, 50)]
plt.plot(xs,[normal_pdf(x,sigma=1) for x in xs],'-',label='mu=0,sigma=1')
plt.plot(xs,[normal_pdf(x,sigma=2) for x in xs],'--',label='mu=0,sigma=2')
plt.plot(xs,[normal_pdf(x,sigma=0.5) for x in xs],':',label='mu=0,sigma=0.5')
plt.plot(xs,[normal_pdf(x,mu=-1) for x in xs],'-.',label='mu=-1,sigma=1')
plt.legend()
plt.title("Various Normal pdfs")
plt.show()

anh

  • Hàm phân phối tích lũy (CDF) của phân phối chuẩn được định nghĩa:
\[F(x|\mu,\sigma) = \displaystyle \int_{-\infty}^{x}f(t|\mu,\sigma)dt\]
  • Không có cách viết đóng dạng “elementary” cho tích phân này, nhưng nó có thể được biểu diễn bằng hàm lỗi (error function, erf), một hàm toán học được định nghĩa như sau:
\[\text{erf}(z) = \frac{2}{\sqrt{\pi}} \displaystyle \int_{0}^{z}\exp(-t^2)dt\]
  • Với phân phối chuẩn chuẩn hóa ($\mu = 0$ và $\sigma = 1$), CDF có thể được biểu diễn qua erf như sau:
\[F(x) = \frac{1}{2}\left(1 + \text{erf}\left(\frac{x - \mu}{\sqrt{2}\sigma}\right)\right)\]
  • Ta có thể code như sau:
1
2

def normal_cdf(x, mu=0,sigma=1):
    return (1 + math.erf((x - mu) / math.sqrt(2) / sigma)) / 2
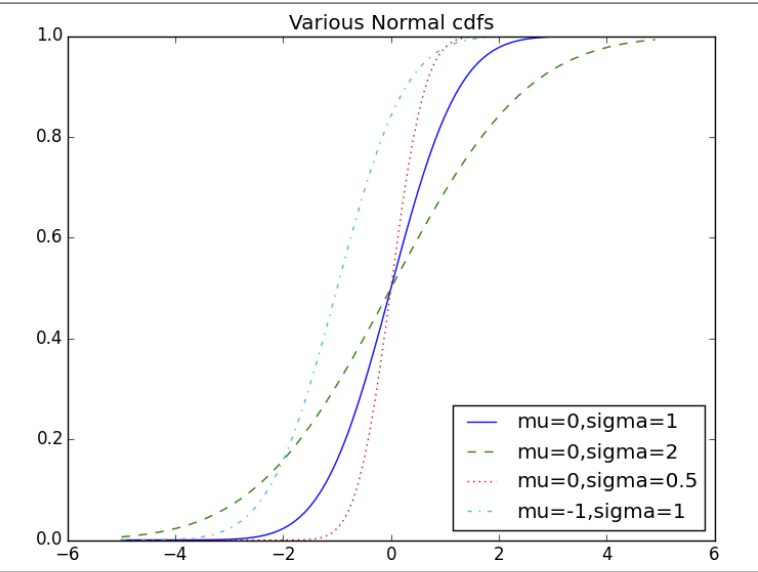
  • Giờ chúng ta hãy thử vẽ đồ thị của một vài giá trị trung bình và độ lệch chuẩn của hà CDF:
1
2
3
4
5
6
7
8

xs = [x / 10.0 for x in range(-50, 50)]
plt.plot(xs,[normal_cdf(x,sigma=1) for x in xs],'-',label='mu=0,sigma=1')
plt.plot(xs,[normal_cdf(x,sigma=2) for x in xs],'--',label='mu=0,sigma=2')
plt.plot(xs,[normal_cdf(x,sigma=0.5) for x in xs],':',label='mu=0,sigma=0.5')
plt.plot(xs,[normal_cdf(x,mu=-1) for x in xs],'-.',label='mu=-1,sigma=1')
plt.legend(loc=4) # bottom right
plt.title("Various Normal cdfs")
plt.show()

anh

Định lý giới hạn trung tâm (The Central Limit Theorem)

  • Một lý do khiến phân phối chuẩn rất hữu ích là định lý giới hạn trung tâm, định lý nói rằng một biến ngẫu nhiên được định nghĩa bằng trung bình của một số lượng lớn các biến ngẫu nhiên độc lập và có phân phối giống nhau sẽ xấp xỉ phân phối chuẩn.
  • Cụ thể, nếu $x_1, \dots , x_n$ là các biến ngẫu nhiên có $\mu$ trung bình và độ lệch chuẩn $\sigma$, và nếu $n$ lớn thì:
\[X = \frac{1}{n}(x_1 + \dots + x_n)\]
  • $X$ Xấp xỉ phân bố chuẩn với $\mu$ trung bình và độ lệch chuẩn $\frac{\sigma}{\sqrt{n}}$. Tương đương với:
\[X = \frac{(x_1 + \dots + x_n) - \mu n}{\sigma\sqrt{n}}\]

  • $X$ ở phương trình trên xấp xỉ phân bố chuẩn với trung bình 0 và độ lệch chuẩn 1.

  • Một cách dễ dàng để minh họa điều này là nhìn vào các biến ngẫu nhiên nhị thức (binomial), có hai tham số $n$ và $p$. Một biến ngẫu nhiên nhị thức ($n$,$p$) chỉ đơn giản là tổng của $n$ biến ngẫu nhiên Bernoulli($p$) độc lập, Bernoulli($p$) được định nghĩa là bằng 1 với xác suất $p$ và 0 với xác suất $1 - p$:

1
2
3
4
5

def bernoulli_trial(p):
    return 1 if random.random() < p else 0
def binomial(n, p):
    return sum(bernoulli_trial(p) for _ in range(n))
  • Một biến ngẫu nhiên Bernoulli($p$) chỉ có hai giá trị khả dĩ: 1 (với xác suất $p$) và 0 (với xác suất $1 - p$)
  • Giá trị kỳ vọng ($\mu$) của biến ngẫu nhiên được tính bằng:
\[\mathbb{E}[X] = 1.p + 0.(1-p) = p\]
  • Độ lệch chuẩn (\sigma) là căn bậc hai của phương sai:
\[\sigma = \sqrt{\text{Var}(X)} = \sqrt{\mathbb{E}[X^2] - (\mathbb{E}[X])^2} \\ \sigma = \sqrt{p - p^2} = \sqrt{p(1 - p)}\]
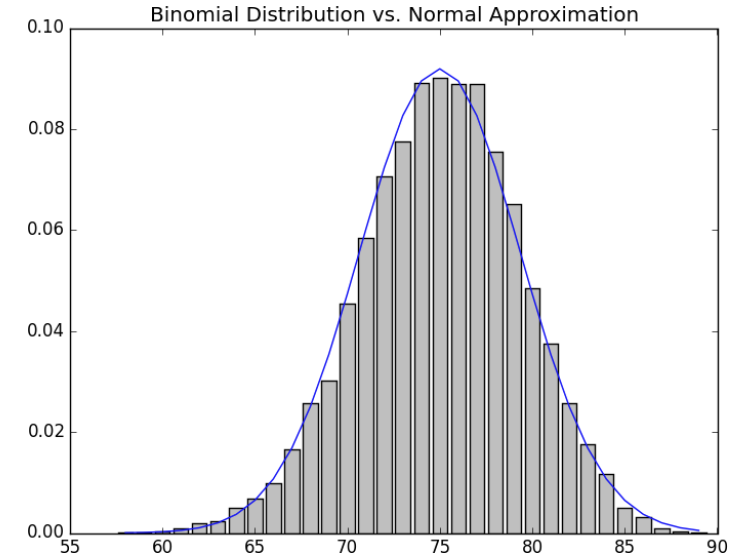
  • Giá trị trung bình của một biến Bernoulli(p) là $p$ và độ lệch chuẩn của nó là $\sqrt{p(1 - p)}$. Định lý giới hạn trung tâm nói rằng khi $n$ trở nên lớn, biến nhị thức ($n$,$p$) (Binomial($n$,$p$))) xấp xỉ một biến ngẫu nhiên theo phân bố chuẩn với trung bình $\mu = np$ và độ lệch chuẩn $\sigma = \sqrt{np(1 - p)}$. Nếu chúng ta vẽ cả hai, bạn có thể dễ dàng thấy sự giống nhau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def make_hist(p, n, num_points):
    data = [binomial(n, p) for _ in range(num_points)]
    # use a bar chart to show the actual binomial samples
    histogram = Counter(data)
    plt.bar([x - 0.4 for x in histogram.keys()],
            [v / num_points for v in histogram.values()],
            0.8,
            color='0.75')
    mu = p * n
    sigma = math.sqrt(n * p * (1 - p))
    # use a line chart to show the normal approximation
    xs = range(min(data), max(data) + 1)
    ys = [normal_cdf(i + 0.5, mu, sigma) - normal_cdf(i - 0.5, mu, sigma)
        for i in xs]
    plt.plot(xs,ys)
    plt.title("Binomial Distribution vs. Normal Approximation")
    plt.show()
  • Khi bạn gọi hàm make_hist(0.75,100,10000), bạn sẽ nhận được đồ thị sau:

anh

3. Tổng kết

  • Xác suất thống kê đóng vai trò quan trọng trong lĩnh vực Machine Learning, cung cấp nền tảng toán học để xử lý dữ liệu, xây dựng và đánh giá mô hình. Các khái niệm như phân phối xác suất, kỳ vọng, phương sai, và các bài toán kiểm định giả thuyết đều hỗ trợ trong việc hiểu và giải quyết các vấn đề thực tế. Trong Machine Learning, xác suất giúp chúng ta xử lý sự không chắc chắn, tối ưu hóa mô hình, và đánh giá độ tin cậy của dự đoán. Việc nắm vững xác suất thống kê không chỉ giúp xây dựng các thuật toán mạnh mẽ mà còn cải thiện khả năng phân tích dữ liệu và đưa ra quyết định hiệu quả.
Machine Learning
statistical probability
This post is licensed under CC BY 4.0 by the author.